This class represents an ideal helix in perigee parameterization. More...

#include <Helix.h>

Inheritance diagram for Helix:

[legend]

Collaboration diagram for Helix:

[legend]

Public Member Functions
	Helix ()
	Constructor initializing all perigee parameters to zero.

	Helix (const ROOT::Math::XYZVector &position, const ROOT::Math::XYZVector &momentum, const short int charge, const double bZ)
	Constructor initializing class with a fit result.

	Helix (const double &d0, const double &phi0, const double &omega, const double &z0, const double &tanLambda)
	Constructor initializing class with perigee parameters.

void	addRelationTo (const RelationsInterface< BASE > *object, float weight=1.0, const std::string &namedRelation="") const
	Add a relation from this object to another object (with caching).

void	addRelationTo (const TObject *object, float weight=1.0, const std::string &namedRelation="") const
	Add a relation from this object to another object (no caching, can be quite slow).

void	copyRelations (const RelationsInterface< BASE > *sourceObj)
	Copies all relations of sourceObj (pointing from or to sourceObj) to this object (including weights).

template<class TO >
RelationVector< TO >	getRelationsTo (const std::string &name="", const std::string &namedRelation="") const
	Get the relations that point from this object to another store array.

template<class FROM >
RelationVector< FROM >	getRelationsFrom (const std::string &name="", const std::string &namedRelation="") const
	Get the relations that point from another store array to this object.

template<class T >
RelationVector< T >	getRelationsWith (const std::string &name="", const std::string &namedRelation="") const
	Get the relations between this object and another store array.

template<class TO >
TO *	getRelatedTo (const std::string &name="", const std::string &namedRelation="") const
	Get the object to which this object has a relation.

template<class FROM >
FROM *	getRelatedFrom (const std::string &name="", const std::string &namedRelation="") const
	Get the object from which this object has a relation.

template<class T >
T *	getRelated (const std::string &name="", const std::string &namedRelation="") const
	Get the object to or from which this object has a relation.

template<class TO >
std::pair< TO *, float >	getRelatedToWithWeight (const std::string &name="", const std::string &namedRelation="") const
	Get first related object & weight of relation pointing to an array.

template<class FROM >
std::pair< FROM *, float >	getRelatedFromWithWeight (const std::string &name="", const std::string &namedRelation="") const
	Get first related object & weight of relation pointing from an array.

template<class T >
std::pair< T *, float >	getRelatedWithWeight (const std::string &name="", const std::string &namedRelation="") const
	Get first related object & weight of relation pointing from/to an array.

virtual std::string	getName () const
	Return a short name that describes this object, e.g.

virtual std::string	getInfoHTML () const
	Return a short summary of this object's contents in HTML format.

std::string	getInfo () const
	Return a short summary of this object's contents in raw text format.

std::string	getArrayName () const
	Get name of array this object is stored in, or "" if not found.

int	getArrayIndex () const
	Returns this object's array index (in StoreArray), or -1 if not found.

Getters for perigee helix parameters
double	getD0 () const
	Getter for d0, which is the signed distance to the perigee in the r-phi plane.

double	getPhi0 () const
	Getter for phi0, which is the azimuth angle of the transverse momentum at the perigee.

double	getCosPhi0 () const
	Getter for the cosine of the azimuth angle of travel direction at the perigee.

double	getSinPhi0 () const
	Getter for the cosine of the azimuth angle of travel direction at the perigee.

double	getOmega () const
	Getter for omega, which is a signed curvature measure of the track.

double	getZ0 () const
	Getter for z0, which is the z coordinate of the perigee.

double	getTanLambda () const
	Getter for tan lambda, which is the z over two dimensional arc length slope of the track.

double	getCotTheta () const
	Getter for cot theta, which is the z over two dimensional arc length slope of the track.

Protected Member Functions
void	calcArcLength2DAndDrAtXY (const double &x, const double &y, double &arcLength2D, double &dr) const
	Helper method to calculate the signed two dimensional arc length and the signed distance to the circle of a point in the xy projection.

double	calcArcLength2DAtDeltaCylindricalRAndDr (const double &deltaCylindricalR, const double &dr) const
	Helper method to calculate the two dimensional arc length from the perigee to a point at cylindrical radius, which also has the distance dr from the circle in the xy projection.

TClonesArray *	getArrayPointer () const
	Returns the pointer to the raw DataStore array holding this object (protected since these arrays are easy to misuse).

Static Protected Member Functions
static double	calcASinXDividedByX (const double &x)
	Implementation of the function asin(x) / x which handles small x values smoothly.

static double	calcATanXDividedByX (const double &x)
	Implementation of the function atan(x) / x which handles small x values smoothly.

static double	calcDerivativeOfATanXDividedByX (const double &x)
	Implementation of the function d / dx (atan(x) / x) which handles small x values smoothly.

Private Member Functions
void	setCartesian (const ROOT::Math::XYZVector &position, const ROOT::Math::XYZVector &momentum, const short int charge, const double bZ)
	Cartesian to Perigee conversion.

	ClassDef (Helix, 2)
	This class represents an ideal helix in perigee parameterization.

Private Attributes
Double32_t	m_d0
	Memory for the signed distance to the perigee.

Double32_t	m_phi0
	Memory for the azimuth angle between the transverse momentum and the x axis, which is in [-pi, pi].

Double32_t	m_omega
	Memory for the curvature of the signed curvature.

Double32_t	m_z0
	Memory for the z coordinate of the perigee.

Double32_t	m_tanLambda
	Memory for the slope of the track in the z coordinate over the two dimensional arc length (dz/ds)

DataStore::StoreEntry *	m_cacheDataStoreEntry
	Cache of the data store entry to which this object belongs.

int	m_cacheArrayIndex
	Cache of the index in the TClonesArray to which this object belongs.

Friends
std::ostream &	operator<< (std::ostream &output, const Helix &helix)
	Output operator for debugging and the generation of unittest error messages.

Getters for cartesian parameters of the perigee
double	getPerigeeX () const
	Calculates the x coordinate of the perigee point.

double	getPerigeeY () const
	Calculates the y coordinate of the perigee point.

double	getPerigeeZ () const
	Calculates the z coordinate of the perigee point.

ROOT::Math::XYZVector	getPerigee () const
	Getter for the perigee position.

double	getMomentumX (const double bZ) const
	Calculates the x momentum of the particle at the perigee point.

double	getMomentumY (const double bZ) const
	Calculates the y momentum of the particle at the perigee point.

double	getMomentumZ (const double bZ) const
	Calculates the z momentum of the particle at the perigee point.

ROOT::Math::XYZVector	getMomentum (const double bZ) const
	Getter for vector of momentum at the perigee position.

ROOT::Math::XYZVector	getDirection () const
	Getter for unit vector of momentum at the perigee position.

double	getTransverseMomentum (const double bZ) const
	Getter for the absolute value of the transverse momentum at the perigee.

double	getKappa (const double bZ) const
	Getter for kappa, which is charge / transverse momentum or equivalently omega * alpha.

short	getChargeSign () const
	Return track charge sign (1, 0 or -1).

static double	getAlpha (const double bZ)
	Calculates the alpha value for a given magnetic field in Tesla.

Simple extrapolations of the ideal helix
double	getArcLength2DAtCylindricalR (const double &cylindricalR) const
	Calculates the transverse travel distance at the point the helix first reaches the given cylindrical radius.

double	getArcLength2DAtXY (const double &x, const double &y) const
	Calculates the two dimensional arc length at which the circle in the xy projection is closest to the point.

double	getArcLength2DAtNormalPlane (const double &x, const double &y, const double &nX, const double &nY) const
	Calculates the arc length to reach a plane parallel to the z axes.

ROOT::Math::XYZVector	getPositionAtArcLength2D (const double &arcLength2D) const
	Calculates the position on the helix at the given two dimensional arc length.

ROOT::Math::XYZVector	getTangentialAtArcLength2D (const double &arcLength2D) const
	Calculates the tangential vector to the helix curve at the given two dimensional arc length.

ROOT::Math::XYZVector	getUnitTangentialAtArcLength2D (const double &arcLength2D) const
	Calculates the unit tangential vector to the helix curve at the given two dimensional arc length.

ROOT::Math::XYZVector	getMomentumAtArcLength2D (const double &arcLength2D, const double &bz) const
	Calculates the momentum vector at the given two dimensional arc length.

double	passiveMoveBy (const ROOT::Math::XYZVector &by)
	Moves origin of the coordinate system (passive transformation) by the given vector.

double	passiveMoveBy (const double &byX, const double &byY, const double &byZ)
	Moves origin of the coordinate system (passive transformation) orthogonal to the z axis by the given vector.

TMatrixD	calcPassiveMoveByJacobian (const ROOT::Math::XYZVector &by, const double expandBelowChi=M_PI/8) const
	Calculate the 5x5 jacobian matrix for the transport of the helix parameters, when moving the origin of the coordinate system to a new location.

void	calcPassiveMoveByJacobian (const double &byX, const double &byY, TMatrixD &jacobian, const double expandBelowChi=M_PI/8) const
	Calculate the jacobian matrix for the transport of the helix parameters, when moving the origin of the coordinate system to a new location.

void	reverse ()
	Reverses the direction of travel of the helix in place.

double	calcArcLength2DFromSecantLength (const double &secantLength2D) const
	Helper function to calculate the two dimensional arc length from the length of a secant.

double	calcSecantLengthToArcLength2DFactor (const double &secantLength2D) const
	Helper function to calculate the factor between the dimensional secant length and the two dimensional arc length as seen in xy projection of the helix.

static double	reversePhi (const double &phi)
	Reverses an azimuthal angle to the opposite direction.

Detailed Description

This class represents an ideal helix in perigee parameterization.

The used perigee parameters are:

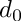
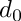
- the signed distance from the origin to the perigee. The sign is positive (negative), if the angle from the xy perigee position vector to the transverse momentum vector is +pi/2 (-pi/2). has the same sign as getPerigee().Cross(getMomentum()).Z().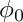
$\phi_0$ - the angle in the xy projection between the transverse momentum and the x axis, which is in [-pi, pi]
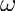
$\omega$ - the signed curvature of the track where the sign is given by the charge of the particle
- z coordinate of the perigee
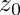
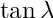
$\tan \lambda$ - the slope of the track in the sz plane (dz/ds)

in that exact order.

Each point on the helix can be adressed by the two dimensional arc length s, which has to be traversed to get to it from the perigee. More precisely the two dimensional arc length means the transverse part of the particles travel distance, hence the arc length of the circle in the xy projection.

If you need different kind of methods / interfaces to the helix please do not hesitate to contact olive.nosp@m.r.fr.nosp@m.ost@d.nosp@m.esy..nosp@m.de Contributions are always welcome.

Definition at line 59 of file Helix.h.

Constructor & Destructor Documentation

◆ Helix() [1/3]

Helix ( )

Constructor initializing all perigee parameters to zero.

Definition at line 24 of file Helix.cc.

            :
  m_d0(0.0),
  m_phi0(0.0),
  m_omega(0.0),
  m_z0(0.0),
  m_tanLambda(0.0)
{
}

◆ Helix() [2/3]

Helix	(	const ROOT::Math::XYZVector &	position,
		const ROOT::Math::XYZVector &	momentum,
		const short int	charge,
		const double	bZ
	)

Constructor initializing class with a fit result.

The given position and momentum are extrapolated to the perigee assuming a homogeneous magnetic field in the z direction.

Parameters

position	Position of the track at the perigee.
momentum	Momentum of the track at the perigee.
charge	Charge of the particle.
bZ	Magnetic field to be used for the calculation of the curvature. It is assumed, that the B-field is homogeneous parallel to the z axis.

Definition at line 33 of file Helix.cc.

{
  setCartesian(position, momentum, charge, bZ);
}

◆ Helix() [3/3]

Helix	(	const double &	d0,
		const double &	phi0,
		const double &	omega,
		const double &	z0,
		const double &	tanLambda
	)

Constructor initializing class with perigee parameters.

Parameters

d0	The signed distance from the origin to the perigee. The sign is positive (negative), if the angle from the xy perigee position vector to the transverse momentum vector is +pi/2 (-pi/2). d0 has the same sign as `getPosition().Cross(getMomentum()).Z()`.
phi0	The angle between the transverse momentum and the x axis and in [-pi, pi].
omega	The signed curvature of the track where the sign is given by the charge of the particle.
z0	The z coordinate of the perigee.
tanLambda	The slope of the track in the sz plane (dz/ds).

Definition at line 41 of file Helix.cc.

  : m_d0(d0),
    m_phi0(phi0),
    m_omega(omega),
    m_z0(z0),
    m_tanLambda(tanLambda)
{
}

Member Function Documentation

◆ addRelationTo() [1/2]

void addRelationTo	(	const RelationsInterface< BASE > *	object,
		float	weight = `1.0`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Add a relation from this object to another object (with caching).

Parameters

object	The object to which the relation should point.
weight	The weight of the relation.
namedRelation	Additional name for the relation, or "" for the default naming

Definition at line 142 of file RelationsObject.h.

    {
      if (object)
        DataStore::Instance().addRelation(this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                                          object, object->m_cacheDataStoreEntry, object->m_cacheArrayIndex, weight, namedRelation);
    }

◆ addRelationTo() [2/2]

void addRelationTo	(	const TObject *	object,
		float	weight = `1.0`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Add a relation from this object to another object (no caching, can be quite slow).

Parameters

object	The object to which the relation should point.
weight	The weight of the relation.
namedRelation	Additional name for the relation, or "" for the default naming

Definition at line 155 of file RelationsObject.h.

    {
      StoreEntry* toEntry = nullptr;
      int toIndex = -1;
      DataStore::Instance().addRelation(this, m_cacheDataStoreEntry, m_cacheArrayIndex, object, toEntry, toIndex, weight, namedRelation);
    }

◆ calcArcLength2DAndDrAtXY()

void calcArcLength2DAndDrAtXY	(	const double &	x,
		const double &	y,
		double &	arcLength2D,
		double &	dr
	)		const

protected

Helper method to calculate the signed two dimensional arc length and the signed distance to the circle of a point in the xy projection.

This function is an implementation detail that prevents some code duplication.

Parameters

	x	X coordinate of the point to which to extrapolate
	y	Y coordinate of the point to which to extrapolate
[out]	arcLength2D	The two dimensional arc length from the perigee at which the closest approach is reached
[out]	dr	Signed distance of the point to circle in the xy projection.

Definition at line 545 of file Helix.cc.

{
  // Prepare common variables
  const double omega = getOmega();
  const double cosPhi0 = getCosPhi0();
  const double sinPhi0 = getSinPhi0();
  const double d0 = getD0();
 
  const double deltaParallel = x * cosPhi0 + y * sinPhi0;
  const double deltaOrthogonal = y * cosPhi0 - x * sinPhi0 + d0;
  const double deltaCylindricalR = hypot(deltaOrthogonal, deltaParallel);
  const double deltaCylindricalRSquared = deltaCylindricalR * deltaCylindricalR;
 
  const double A = 2 * deltaOrthogonal + omega * deltaCylindricalRSquared;
  const double U = sqrt(1 + omega * A);
  const double UOrthogonal = 1 + omega * deltaOrthogonal; // called nu in the Karimaki paper.
  const double UParallel = omega * deltaParallel;
  // Note U is a vector pointing from the middle of the projected circle scaled by a factor omega.
 
  // Calculate dr
  dr = A / (1 + U);
 
  // Calculate the absolute value of the arc length
  const double chi = -atan2(UParallel, UOrthogonal);
 
  if (fabs(chi) < M_PI / 8) { // Rough guess where the critical zone for approximations begins
    // Close side of the circle
    double principleArcLength2D = deltaParallel / UOrthogonal;
    arcLength2D = principleArcLength2D * calcATanXDividedByX(principleArcLength2D * omega);
  } else {
    // Far side of the circle
    // If the far side of the circle is a well definied concept meaning that we have big enough omega.
    arcLength2D = -chi / omega;
  }
}

◆ calcArcLength2DAtDeltaCylindricalRAndDr()

double calcArcLength2DAtDeltaCylindricalRAndDr	(	const double &	deltaCylindricalR,
		const double &	dr
	)		const

protected

Helper method to calculate the two dimensional arc length from the perigee to a point at cylindrical radius, which also has the distance dr from the circle in the xy projection.

This function is an implementation detail that prevents some code duplication.

Parameters

deltaCylindricalR	The absolute distance of the point in question to the perigee in the xy projection
dr	Signed distance of the point to circle in the xy projection.

Returns: The absolute two dimensional arc length from the perigee to the point.

Definition at line 581 of file Helix.cc.

{
  const double omega = getOmega();
  double secantLength = sqrt((deltaCylindricalR + dr) * (deltaCylindricalR - dr) / (1 + dr * omega));
  return calcArcLength2DFromSecantLength(secantLength);
}

◆ calcArcLength2DFromSecantLength()

double calcArcLength2DFromSecantLength ( const double & secantLength2D ) const

Helper function to calculate the two dimensional arc length from the length of a secant.

Translates the direct length between two point on the circle in the xy projection to the two dimensional arc length on the circle Behaves smoothly in the limit of vanishing curvature.

Definition at line 426 of file Helix.cc.

{
  return secantLength * calcSecantLengthToArcLength2DFactor(secantLength);
}

◆ calcASinXDividedByX()

double calcASinXDividedByX ( const double & x )

staticprotected

Implementation of the function asin(x) / x which handles small x values smoothly.

Definition at line 438 of file Helix.cc.

{
  // Approximation of asin(x) / x
  // Inspired by BOOST's sinc
 
  BOOST_MATH_STD_USING;
 
  auto const taylor_n_bound = boost::math::tools::forth_root_epsilon<double>();
 
  if (abs(x) >= taylor_n_bound) {
    if (fabs(x) == 1) {
      return  M_PI / 2.0;
 
    } else {
      return asin(x) / x;
 
    }
 
  } else {
    // approximation by taylor series in x at 0 up to order 0
    double result = 1.0;
 
    auto const taylor_0_bound = boost::math::tools::epsilon<double>();
    if (abs(x) >= taylor_0_bound) {
      double x2 = x * x;
      // approximation by taylor series in x at 0 up to order 2
      result += x2 / 6.0;
 
      auto const taylor_2_bound = boost::math::tools::root_epsilon<double>();
      if (abs(x) >= taylor_2_bound) {
        // approximation by taylor series in x at 0 up to order 4
        result += x2 * x2 * (3.0 / 40.0);
      }
    }
    return result;
  }
 
}

◆ calcATanXDividedByX()

double calcATanXDividedByX ( const double & x )

staticprotected

Implementation of the function atan(x) / x which handles small x values smoothly.

Definition at line 477 of file Helix.cc.

{
  // Approximation of atan(x) / x
  // Inspired by BOOST's sinc
 
  BOOST_MATH_STD_USING;
 
  auto const taylor_n_bound = boost::math::tools::forth_root_epsilon<double>();
 
  if (abs(x) >= taylor_n_bound) {
    return atan(x) / x;
 
  } else {
    // approximation by taylor series in x at 0 up to order 0
    double result = 1.0;
 
    auto const taylor_0_bound = boost::math::tools::epsilon<double>();
    if (abs(x) >= taylor_0_bound) {
      double x2 = x * x;
      // approximation by taylor series in x at 0 up to order 2
      result -= x2 / 3.0;
 
      auto const taylor_2_bound = boost::math::tools::root_epsilon<double>();
      if (abs(x) >= taylor_2_bound) {
        // approximation by taylor series in x at 0 up to order 4
        result += x2 * x2 * (1.0 / 5.0);
      }
    }
    return result;
  }
}

◆ calcDerivativeOfATanXDividedByX()

double calcDerivativeOfATanXDividedByX ( const double & x )

staticprotected

Implementation of the function d / dx (atan(x) / x) which handles small x values smoothly.

Definition at line 509 of file Helix.cc.

{
  // Approximation of atan(x) / x
  // Inspired by BOOST's sinc
 
  BOOST_MATH_STD_USING;
 
  auto const taylor_n_bound = boost::math::tools::forth_root_epsilon<double>();
 
  const double x2 = x * x;
  if (abs(x) >= taylor_n_bound) {
    const double chi = atan(x);
    return ((1 - chi / x) / x - chi) / (1 + x2);
 
  } else {
    // approximation by taylor series in x at 0 up to order 0
    double result = 1.0;
 
    auto const taylor_0_bound = boost::math::tools::epsilon<double>();
    if (abs(x) >= taylor_0_bound) {
      // approximation by taylor series in x at 0 up to order 2
      result -= 2.0 * x / 3.0;
 
      auto const taylor_2_bound = boost::math::tools::root_epsilon<double>();
      if (abs(x) >= taylor_2_bound) {
        // approximation by taylor series in x at 0 up to order 4
        result += x2 * x * (4.0 / 5.0);
      }
    }
    return result;
  }
}

◆ calcPassiveMoveByJacobian() [1/2]

void calcPassiveMoveByJacobian	(	const double &	byX,
		const double &	byY,
		TMatrixD &	jacobian,
		const double	expandBelowChi = `M_PI / 8`
	)		const

Calculate the jacobian matrix for the transport of the helix parameters, when moving the origin of the coordinate system to a new location.

Does not update the helix parameters in any way.

The jacobian matrix is written into the output parameter 'jacobian'. If output parameter is a 5x5 matrix only the derivatives of the 5 helix parameters are written If output parameter is a 6x6 matrix the derivatives of the 5 helix parameters and derivates of the two dimensional arc length are written. The derivatives of the arcLength2D are in the 6th row of the matrix.

Parameters

	byX	X displacement by which the origin of the coordinate system should be moved.
	byY	Y displacement by which the origin of the coordinate system should be moved.
[out]	jacobian	The jacobian matrix containing the derivatives of the five helix parameters after the move relative the orignal parameters.
	expandBelowChi	Control parameter below, which absolute value of chi an expansion of divergent terms shall be used. This parameter exists for testing the consistency of the expansion with the closed form. In other applications the parameter should remain at its default value.

Definition at line 309 of file Helix.cc.

{
  // 0. Preparations
  // Initialise the return value to a unit matrix
  jacobian.UnitMatrix();
  assert(jacobian.GetNrows() == jacobian.GetNcols());
  assert(jacobian.GetNrows() == 5 or jacobian.GetNrows() == 6);
 
  // Fetch the helix parameters
  const double omega = getOmega();
  const double cosPhi0 = getCosPhi0();
  const double sinPhi0 = getSinPhi0();
  const double d0 = getD0();
  const double tanLambda = getTanLambda();
 
  // Prepare a delta vector, which is the vector from the perigee point to the new origin
  // Split it in component parallel and a component orthogonal to tangent at the perigee.
  const double deltaParallel = byX * cosPhi0 + byY * sinPhi0;
  const double deltaOrthogonal = byY * cosPhi0 - byX * sinPhi0 + d0;
  const double deltaCylindricalR = hypot(deltaOrthogonal, deltaParallel);
  const double deltaCylindricalRSquared = deltaCylindricalR * deltaCylindricalR;
 
  // Some commonly used terms - compare Karimaki 1990
  const double A = 2 * deltaOrthogonal + omega * deltaCylindricalRSquared;
  const double USquared = 1 + omega * A;
  const double U = sqrt(USquared);
  const double UOrthogonal = 1 + omega * deltaOrthogonal; // called nu in the Karimaki paper.
  const double UParallel = omega * deltaParallel;
  // Note U is a vector pointing from the middle of the projected circle scaled by a factor omega.
  const double u = 1 + omega * d0; // just called u in the Karimaki paper.
 
  // ---------------------------------------------------------------------------------------
  // 1. Set the parts related to the xy coordinates
  // Fills the upper left 3x3 corner of the jacobain
 
  // a. Calculate the row related to omega
  // The row related to omega is not different from the unit jacobian initialised above.
  // jacobian(iOmega, iOmega) = 1.0; // From UnitMatrix above.
 
  // b. Calculate the row related to d0
  const double new_d0 = A / (1 + U);
 
  jacobian(iD0, iOmega) = (deltaCylindricalR + new_d0) * (deltaCylindricalR - new_d0) / 2 / U;
  jacobian(iD0, iPhi0) = - u * deltaParallel / U;
  jacobian(iD0, iD0) =  UOrthogonal / U;
 
  // c. Calculate the row related to phi0
  // Also calculate the derivatives of the arc length
  // which are need for the row related to z.
  const double dArcLength2D_dD0 = - UParallel / USquared;
  const double dArcLength2D_dPhi0 = (omega * deltaCylindricalRSquared + deltaOrthogonal - d0 * UOrthogonal) / USquared;
 
  jacobian(iPhi0, iD0) = - dArcLength2D_dD0 * omega;
  jacobian(iPhi0, iPhi0) = u * UOrthogonal / USquared;
  jacobian(iPhi0, iOmega) =  -deltaParallel / USquared;
 
  // For jacobian(iPhi0, iOmega) we have to dig deeper
  // since the normal equations have a divergence for omega -> 0.
  // This hinders not only the straight line case but extrapolations between points which are close together,
  // like it happens when the current perigee is very close the new perigee.
  // To have a smooth transition in this limit we have to carefully
  // factor out the divergent quotients and approximate them with their taylor series.
 
  const double chi = -atan2(UParallel, UOrthogonal);
  double arcLength2D = 0;
  double dArcLength2D_dOmega = 0;
 
  if (fabs(chi) < std::min(expandBelowChi, M_PI / 2.0)) {
    // Never expand for the far side of the circle by limiting the expandBelow to maximally half a pi.
    // Close side of the circle
    double principleArcLength2D = deltaParallel / UOrthogonal;
    const double dPrincipleArcLength2D_dOmega = - principleArcLength2D * deltaOrthogonal / UOrthogonal;
 
    const double x = principleArcLength2D * omega;
    const double f = calcATanXDividedByX(x);
    const double df_dx = calcDerivativeOfATanXDividedByX(x);
 
    arcLength2D = principleArcLength2D * f;
    dArcLength2D_dOmega = (f + x * df_dx) * dPrincipleArcLength2D_dOmega + principleArcLength2D * df_dx * principleArcLength2D;
  } else {
    // Far side of the circle
    // If the far side of the circle is a well definied concept, omega is high enough that
    // we can divide by it.
    // Otherwise nothing can rescue us since the far side of the circle is so far away that no reasonable extrapolation can be made.
    arcLength2D = - chi / omega;
    dArcLength2D_dOmega = (-arcLength2D - jacobian(iPhi0, iOmega)) / omega;
  }
 
  // ---------------------------------------------------------------------------------------
  // 2. Set the parts related to the z coordinate
  // Since tanLambda stays the same there are no entries for tanLambda in the jacobian matrix
  // For the new z0' = z0 + arcLength2D * tanLambda
  jacobian(iZ0, iD0) = tanLambda * dArcLength2D_dD0;
  jacobian(iZ0, iPhi0) = tanLambda * dArcLength2D_dPhi0;
  jacobian(iZ0, iOmega) = tanLambda * dArcLength2D_dOmega;
  jacobian(iZ0, iZ0) = 1.0; // From UnitMatrix above.
  jacobian(iZ0, iTanLambda) = arcLength2D;
 
  if (jacobian.GetNrows() == 6) {
    // Also write the derivates of arcLength2D to the jacobian if the matrix size has space for them.
    jacobian(iArcLength2D, iD0) = dArcLength2D_dD0;
    jacobian(iArcLength2D, iPhi0) = dArcLength2D_dPhi0;
    jacobian(iArcLength2D, iOmega) = dArcLength2D_dOmega;
    jacobian(iArcLength2D, iZ0) = 0.0;
    jacobian(iArcLength2D, iTanLambda) = 0;
    jacobian(iArcLength2D, iArcLength2D) = 1.0;
  }
}

◆ calcPassiveMoveByJacobian() [2/2]

TMatrixD calcPassiveMoveByJacobian	(	const ROOT::Math::XYZVector &	by,
		const double	expandBelowChi = `M_PI / 8`
	)		const

Calculate the 5x5 jacobian matrix for the transport of the helix parameters, when moving the origin of the coordinate system to a new location.

Does not update the helix parameters in any way.

Parameters

by	Vector by which the origin of the coordinate system should be moved.
expandBelowChi	Control parameter below, which absolute value of chi an expansion of divergent terms shall be used. This parameter exists for testing the consistency of the expansion with the closed form. In other applications the parameter should remain at its default value.

Returns: The jacobian matrix containing the derivatives of the five helix parameters after the move relative the orignal parameters.

Definition at line 301 of file Helix.cc.

{
  TMatrixD jacobian(5, 5);
  calcPassiveMoveByJacobian(by.X(), by.Y(), jacobian, expandBelowChi);
  return jacobian;
}

◆ calcSecantLengthToArcLength2DFactor()

double calcSecantLengthToArcLength2DFactor ( const double & secantLength2D ) const

Helper function to calculate the factor between the dimensional secant length and the two dimensional arc length as seen in xy projection of the helix.

Definition at line 432 of file Helix.cc.

{
  double x = secantLength * getOmega() / 2.0;
  return calcASinXDividedByX(x);
}

◆ copyRelations()

void copyRelations ( const RelationsInterface< BASE > * sourceObj )

inlineinherited

Copies all relations of sourceObj (pointing from or to sourceObj) to this object (including weights).

Useful if you want to make a complete copy of a StoreArray object to make modifications to it, but retain all information on linked objects.

Note: this only works if sourceObj inherits from the same base (e.g. RelationsObject), and only for related objects that also inherit from the same base.

Definition at line 170 of file RelationsObject.h.

    {
      if (!sourceObj)
        return;
      auto fromRels = sourceObj->getRelationsFrom<RelationsInterface<BASE>>("ALL");
      for (unsigned int iRel = 0; iRel < fromRels.size(); iRel++) {
        fromRels.object(iRel)->addRelationTo(this, fromRels.weight(iRel));
      }
 
      auto toRels = sourceObj->getRelationsTo<RelationsInterface<BASE>>("ALL");
      for (unsigned int iRel = 0; iRel < toRels.size(); iRel++) {
        this->addRelationTo(toRels.object(iRel), toRels.weight(iRel));
      }
    }

◆ getAlpha()

double getAlpha ( const double bZ )

static

Calculates the alpha value for a given magnetic field in Tesla.

Definition at line 109 of file Helix.cc.

{
  return 1.0 / (bZ * Const::speedOfLight) * 1E4;
}

◆ getArcLength2DAtCylindricalR()

double getArcLength2DAtCylindricalR ( const double & cylindricalR ) const

Calculates the transverse travel distance at the point the helix first reaches the given cylindrical radius.

Gives the two dimensional arc length in the forward direction that is traversed until a certain cylindrical radius is reached. Returns NAN, if the cylindrical radius can not be reached, either because it is to far outside or inside of the perigee.

Forward the result to getPositionAtArcLength2D() or getMomentumAtArcLength2D() in order to extrapolate to the cylinder detector boundaries.

The result always has a positive sign. Hence it refers to the forward direction. Adding a minus sign yields the point at the same cylindrical radius but in the backward direction.

Parameters

cylindricalR The cylinder radius to extrapolate to.

Returns: The two dimensional arc length traversed to reach the cylindrical radius. NAN if it can not be reached.

Definition at line 128 of file Helix.cc.

{
  // Slight trick here
  // Since the sought point is on the helix we treat it as the perigee
  // and the origin as the point to extrapolate to.
  // We know the distance of the origin to the circle, which is just d0
  // The direct distance from the origin to the imaginary perigee is just the given cylindricalR.
  const double dr = getD0();
  const double deltaCylindricalR = cylindricalR;
  const double absArcLength2D = calcArcLength2DAtDeltaCylindricalRAndDr(deltaCylindricalR, dr);
  return absArcLength2D;
}

◆ getArcLength2DAtNormalPlane()

double getArcLength2DAtNormalPlane	(	const double &	x,
		const double &	y,
		const double &	nX,
		const double &	nY
	)		const

Calculates the arc length to reach a plane parallel to the z axes.

If there is no intersection with the plane NAN is returned

Parameters

x	X coordinate of the support point of the plane
y	Y coordinate of the support point of the plane
nX	X coordinate of the normal vector of the plane
nY	Y coordinate of the normal vector of the plane

Returns: Shortest two dimensional arc length to the plane

Definition at line 149 of file Helix.cc.

{
  // Construct the tangential vector to the plan in xy space
  const double tX = nY;
  const double tY = -nX;
 
  // Fetch the helix parameters
  const double omega = getOmega();
  const double cosPhi0 = getCosPhi0();
  const double sinPhi0 = getSinPhi0();
  const double d0 = getD0();
 
  // Prepare a delta vector, which is the vector from the perigee point to the support point of the plane
  // Split it in component parallel and a component orthogonal to tangent at the perigee.
  const double deltaParallel = byX * cosPhi0 + byY * sinPhi0;
  const double deltaOrthogonal = byY * cosPhi0 - byX * sinPhi0 + d0;
  const double deltaCylindricalR = hypot(deltaOrthogonal, deltaParallel);
  const double deltaCylindricalRSquared = deltaCylindricalR * deltaCylindricalR;
 
  const double UOrthogonal = 1 + omega * deltaOrthogonal; // called nu in the Karimaki paper.
  const double UParallel = omega * deltaParallel;
 
  // Some commonly used terms - compare Karimaki 1990
  const double A = 2 * deltaOrthogonal + omega * deltaCylindricalRSquared;
 
  const double tParallel = tX * cosPhi0 + tY * sinPhi0;
  const double tOrthogonal = tY * cosPhi0 - tX * sinPhi0;
  const double tCylindricalR = (tX * tX + tY * tY);
 
  const double c = A / 2;
  const double b = UParallel * tParallel + UOrthogonal * tOrthogonal;
  const double a = omega / 2 * tCylindricalR;
 
  const double discriminant = ((double)b) * b - 4 * a * c;
  const double root = sqrt(discriminant);
  const double bigSum = (b > 0) ? -b - root : -b + root;
 
  const double bigOffset = bigSum / 2 / a;
  const double smallOffset = 2 * c / bigSum;
 
  const double distance1 = hypot(byX + bigOffset   * tX, byY + bigOffset   * tY);
  const double distance2 = hypot(byX + smallOffset * tX, byY + smallOffset * tY);
 
  if (distance1 < distance2) {
    return getArcLength2DAtXY(byX + bigOffset   * tX, byY + bigOffset   * tY);
  } else {
    return getArcLength2DAtXY(byX + smallOffset * tX, byY + smallOffset * tY);
  }
}

◆ getArcLength2DAtXY()

double getArcLength2DAtXY	(	const double &	x,
		const double &	y
	)		const

Calculates the two dimensional arc length at which the circle in the xy projection is closest to the point.

This calculates the dimensional arc length to the closest approach in xy projection. Hence, it only optimizes the distance in x and y. This is sufficent to extrapolate to an axial wire. For stereo wires this is not optimal, since the distance in the z direction also plays a role.

Parameters

x	X coordinate of the point to which to extrapolate
y	Y coordinate of the point to which to extrapolate

Returns: The two dimensional arc length from the perigee at which the closest approach is reached

Definition at line 141 of file Helix.cc.

{
  double dr = 0;
  double arcLength2D = 0;
  calcArcLength2DAndDrAtXY(x, y, arcLength2D, dr);
  return arcLength2D;
}

◆ getArrayIndex()

int getArrayIndex ( ) const

inlineinherited

Returns this object's array index (in StoreArray), or -1 if not found.

Definition at line 385 of file RelationsObject.h.

    {
      DataStore::Instance().findStoreEntry(this, m_cacheDataStoreEntry, m_cacheArrayIndex);
      return m_cacheArrayIndex;
    }

◆ getArrayName()

std::string getArrayName ( ) const

inlineinherited

Get name of array this object is stored in, or "" if not found.

Definition at line 377 of file RelationsObject.h.

    {
      DataStore::Instance().findStoreEntry(this, m_cacheDataStoreEntry, m_cacheArrayIndex);
      return m_cacheDataStoreEntry ? m_cacheDataStoreEntry->name : "";
    }

◆ getArrayPointer()

TClonesArray * getArrayPointer ( ) const

inlineprotectedinherited

Returns the pointer to the raw DataStore array holding this object (protected since these arrays are easy to misuse).

Definition at line 418 of file RelationsObject.h.

    {
      DataStore::Instance().findStoreEntry(this, m_cacheDataStoreEntry, m_cacheArrayIndex);
      if (!m_cacheDataStoreEntry)
        return nullptr;
      return m_cacheDataStoreEntry->getPtrAsArray();
    }

◆ getChargeSign()

short getChargeSign ( ) const

Return track charge sign (1, 0 or -1).

Definition at line 114 of file Helix.cc.

{
  return boost::math::sign(getOmega());
}

◆ getCosPhi0()

double getCosPhi0 ( ) const

inline

Getter for the cosine of the azimuth angle of travel direction at the perigee.

Definition at line 381 of file Helix.h.

381{ return std::cos(getPhi0()); }

Belle2::Helix::getPhi0

double getPhi0() const

Getter for phi0, which is the azimuth angle of the transverse momentum at the perigee.

Definition: Helix.h:378

◆ getCotTheta()

double getCotTheta ( ) const

inline

Getter for cot theta, which is the z over two dimensional arc length slope of the track.

Synomym to tan lambda.

Definition at line 396 of file Helix.h.

396{ return m_tanLambda; }

◆ getD0()

double getD0 ( ) const

inline

Getter for d0, which is the signed distance to the perigee in the r-phi plane.

The signed distance from the origin to the perigee. The sign is positive (negative), if the angle from the xy perigee position vector to the transverse momentum vector is +pi/2 (-pi/2). d0 has the same sign as getPerigee().Cross(getMomentum()).Z().

Definition at line 372 of file Helix.h.

372{ return m_d0; }

◆ getDirection()

ROOT::Math::XYZVector getDirection ( ) const

Getter for unit vector of momentum at the perigee position.

This is mainly useful cases where curvature is zero (pT is infinite)

Definition at line 94 of file Helix.cc.

{
  return ROOT::Math::XYZVector(getCosPhi0(), getSinPhi0(), getTanLambda());
}

◆ getInfo()

std::string getInfo ( ) const

inlineinherited

Return a short summary of this object's contents in raw text format.

Returns the contents of getInfoHTML() while translating line-breaks etc.

Note: : You don't need to implement this function (it's not virtual), getInfoHTML() is enough.

Definition at line 370 of file RelationsObject.h.

    {
      return _RelationsInterfaceImpl::htmlToPlainText(getInfoHTML());
    }

◆ getInfoHTML()

virtual std::string getInfoHTML ( ) const

inlinevirtualinherited

Return a short summary of this object's contents in HTML format.

Reimplement this in your own class to provide useful output for display or debugging purposes. For example, you might do something like:

std::stringstream out;
out << "<b>PDG</b>: " << m_pdg << "<br>";
out << "<b>Covariance Matrix</b>: " << HTML::getString(getCovariance5()) << "<br>";
return out.str();

See also: Particle::getInfoHTML() for a more complex example.; HTML for some utility functions.; Use getInfo() to get a raw text version of this output.

Reimplemented in Particle, Cluster, MCParticle, PIDLikelihood, SoftwareTriggerResult, Track, TrackFitResult, and TRGSummary.

Definition at line 362 of file RelationsObject.h.

362{ return ""; }

◆ getKappa()

double getKappa ( const double bZ ) const

Getter for kappa, which is charge / transverse momentum or equivalently omega * alpha.

Definition at line 104 of file Helix.cc.

{
  return getOmega() * getAlpha(bZ);
}

◆ getMomentum()

ROOT::Math::XYZVector getMomentum ( const double bZ ) const

Getter for vector of momentum at the perigee position.

As we calculate recalculate the momentum from a geometric helix, we need an estimate of the magnetic field along the z-axis to give back the momentum.

Parameters

bZ	Magnetic field at the perigee.

Definition at line 89 of file Helix.cc.

{
  return ROOT::Math::XYZVector(getMomentumX(bZ), getMomentumY(bZ), getMomentumZ(bZ));
}

◆ getMomentumAtArcLength2D()

ROOT::Math::XYZVector getMomentumAtArcLength2D	(	const double &	arcLength2D,
		const double &	bz
	)		const

Calculates the momentum vector at the given two dimensional arc length.

Parameters

arcLength2D	Two dimensional arc length to be traversed.
bz	Magnetic field strength in the z direction.

Definition at line 270 of file Helix.cc.

{
  ROOT::Math::XYZVector momentum = getTangentialAtArcLength2D(arcLength2D);
  const double pr = getTransverseMomentum(bz);
  momentum *= pr;
 
  return momentum;
}

◆ getMomentumX()

double getMomentumX ( const double bZ ) const

Calculates the x momentum of the particle at the perigee point.

Parameters

bZ	Z component of the magnetic field in Tesla

Definition at line 74 of file Helix.cc.

{
  return getCosPhi0() * getTransverseMomentum(bZ);
}

◆ getMomentumY()

double getMomentumY ( const double bZ ) const

Calculates the y momentum of the particle at the perigee point.

Parameters

bZ	Z component of the magnetic field in Tesla

Definition at line 79 of file Helix.cc.

{
  return getSinPhi0() * getTransverseMomentum(bZ);
}

◆ getMomentumZ()

double getMomentumZ ( const double bZ ) const

Calculates the z momentum of the particle at the perigee point.

Parameters

bZ	Z component of the magnetic field in Tesla

Definition at line 84 of file Helix.cc.

{
  return getTanLambda() * getTransverseMomentum(bZ);
}

◆ getName()

virtual std::string getName ( ) const

inlinevirtualinherited

Return a short name that describes this object, e.g.

pi+ for an MCParticle.

Reimplemented in Particle, and MCParticle.

Definition at line 344 of file RelationsObject.h.

344{ return ""; }

◆ getOmega()

double getOmega ( ) const

inline

Getter for omega, which is a signed curvature measure of the track.

The sign is equivalent to the charge of the particle.

Definition at line 387 of file Helix.h.

387{ return m_omega; }

◆ getPerigee()

ROOT::Math::XYZVector getPerigee ( ) const

Getter for the perigee position.

Definition at line 69 of file Helix.cc.

{
  return ROOT::Math::XYZVector(getPerigeeX(), getPerigeeY(), getPerigeeZ());
}

◆ getPerigeeX()

double getPerigeeX ( ) const

Calculates the x coordinate of the perigee point.

Definition at line 54 of file Helix.cc.

{
  return getD0() * getSinPhi0();
}

◆ getPerigeeY()

double getPerigeeY ( ) const

Calculates the y coordinate of the perigee point.

Definition at line 59 of file Helix.cc.

{
  return -getD0() * getCosPhi0();
}

◆ getPerigeeZ()

double getPerigeeZ ( ) const

Calculates the z coordinate of the perigee point.

Definition at line 64 of file Helix.cc.

{
  return getZ0();
}

◆ getPhi0()

double getPhi0 ( ) const

inline

Getter for phi0, which is the azimuth angle of the transverse momentum at the perigee.

getMomentum().Phi() == getPhi0() holds.

Definition at line 378 of file Helix.h.

378{ return m_phi0; }

◆ getPositionAtArcLength2D()

ROOT::Math::XYZVector getPositionAtArcLength2D ( const double & arcLength2D ) const

Calculates the position on the helix at the given two dimensional arc length.

Parameters

arcLength2D Two dimensional arc length to be traversed.

Definition at line 201 of file Helix.cc.

{
  /*
    /   \     /                      \     /                              \
    | x |     | cos phi0   -sin phi0 |     |    - sin(chi)  / omega       |
    |   |  =  |                      |  *  |                              |
    | y |     | sin phi0    cos phi0 |     | -(1 - cos(chi)) / omega - d0 |
    \   /     \                      /     \                              /
 
    and
 
    z = tanLambda * arclength + z0;
 
    where chi = -arcLength2D * omega
 
    Here arcLength2D means the arc length of the circle in the xy projection
    traversed in the forward direction.
  */
 
  // First calculating the position assuming the circle center lies on the y axes (phi0 = 0)
  // Rotate to the right phi position afterwards
  // Using the sinus cardinalis yields expressions that are smooth in the limit of omega -> 0
 
  // Do calculations in double
  const double chi = -arcLength2D * getOmega();
  const double chiHalf = chi / 2.0;
 
  using boost::math::sinc_pi;
 
  const double x = arcLength2D * sinc_pi(chi);
  const double y = arcLength2D * sinc_pi(chiHalf) * sin(chiHalf) - getD0();
 
  // const double z = s * tan lambda + z0
  const double z = fma((double)arcLength2D, getTanLambda(),  getZ0());
 
  // Unrotated position
  ROOT::Math::XYZVector position(x, y, z);
 
  // Rotate to the right phi0 position
  position = ROOT::Math::VectorUtil::RotateZ(position, getPhi0());
 
  return position;
}

◆ getRelated()

T * getRelated	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the object to or from which this object has a relation.

Template Parameters

T	The class of objects to or from which the relation points.

Parameters

name	The name of the store array to or from which the relation points. If empty the default store array name for class T will be used. If the special name "ALL" is given all store arrays containing objects of type T are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: The first related object or a null pointer.

Definition at line 278 of file RelationsObject.h.

    {
      return static_cast<T*>(DataStore::Instance().getRelationWith(DataStore::c_BothSides, this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                             T::Class(), name, namedRelation).object);
    }

◆ getRelatedFrom()

FROM * getRelatedFrom	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the object from which this object has a relation.

Template Parameters

FROM	The class of objects from which the relation points.

Parameters

name	The name of the store array from which the relation points. If empty the default store array name for class FROM will be used. If the special name "ALL" is given all store arrays containing objects of type FROM are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: The first related object or a null pointer.

Definition at line 263 of file RelationsObject.h.

    {
      return static_cast<FROM*>(DataStore::Instance().getRelationWith(DataStore::c_FromSide, this, m_cacheDataStoreEntry,
                                m_cacheArrayIndex, FROM::Class(), name, namedRelation).object);
    }

◆ getRelatedFromWithWeight()

std::pair< FROM *, float > getRelatedFromWithWeight	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get first related object & weight of relation pointing from an array.

Template Parameters

FROM	The class of objects from which the relation points.

Parameters

name	The name of the store array from which the relation points. If empty the default store array name for class FROM will be used. If the special name "ALL" is given all store arrays containing objects of type FROM are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: Pair of first related object and the relation weight, or (NULL, 1.0) if none found.

Definition at line 314 of file RelationsObject.h.

    {
      RelationEntry entry = DataStore::Instance().getRelationWith(DataStore::c_FromSide, this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                                                                  FROM::Class(), name, namedRelation);
      return std::make_pair(static_cast<FROM*>(entry.object), entry.weight);
    }

◆ getRelatedTo()

TO * getRelatedTo	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the object to which this object has a relation.

Template Parameters

TO	The class of objects to which the relation points.

Parameters

name	The name of the store array to which the relation points. If empty the default store array name for class TO will be used. If the special name "ALL" is given all store arrays containing objects of type TO are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: The first related object or a null pointer.

Definition at line 248 of file RelationsObject.h.

    {
      return static_cast<TO*>(DataStore::Instance().getRelationWith(DataStore::c_ToSide, this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                              TO::Class(), name, namedRelation).object);
    }

◆ getRelatedToWithWeight()

std::pair< TO *, float > getRelatedToWithWeight	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get first related object & weight of relation pointing to an array.

Template Parameters

TO	The class of objects to which the relation points.

Parameters

name	The name of the store array to which the relation points. If empty the default store array name for class TO will be used. If the special name "ALL" is given all store arrays containing objects of type TO are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: Pair of first related object and the relation weight, or (NULL, 1.0) if none found.

Definition at line 297 of file RelationsObject.h.

    {
      RelationEntry entry = DataStore::Instance().getRelationWith(DataStore::c_ToSide, this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                                                                  TO::Class(), name, namedRelation);
      return std::make_pair(static_cast<TO*>(entry.object), entry.weight);
    }

◆ getRelatedWithWeight()

std::pair< T *, float > getRelatedWithWeight	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get first related object & weight of relation pointing from/to an array.

Template Parameters

T	The class of objects to or from which the relation points.

Parameters

name	The name of the store array to or from which the relation points. If empty the default store array name for class T will be used. If the special name "ALL" is given all store arrays containing objects of type T are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: Pair of first related object and the relation weight, or (NULL, 1.0) if none found.

Definition at line 331 of file RelationsObject.h.

    {
      RelationEntry entry = DataStore::Instance().getRelationWith(DataStore::c_BothSides, this, m_cacheDataStoreEntry, m_cacheArrayIndex,
                                                                  T::Class(), name, namedRelation);
      return std::make_pair(static_cast<T*>(entry.object), entry.weight);
    }

◆ getRelationsFrom()

RelationVector< FROM > getRelationsFrom	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the relations that point from another store array to this object.

Template Parameters

FROM	The class of objects from which the relations point.

Parameters

name	The name of the store array from which the relations point. If empty the default store array name for class FROM will be used. If the special name "ALL" is given all store arrays containing objects of type FROM are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: A vector of relations.

Definition at line 212 of file RelationsObject.h.

    {
      return RelationVector<FROM>(DataStore::Instance().getRelationsWith(DataStore::c_FromSide, this, m_cacheDataStoreEntry,
                                  m_cacheArrayIndex, FROM::Class(), name, namedRelation));
    }

◆ getRelationsTo()

RelationVector< TO > getRelationsTo	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the relations that point from this object to another store array.

Template Parameters

TO	The class of objects to which the relations point.

Parameters

name	The name of the store array to which the relations point. If empty the default store array name for class TO will be used. If the special name "ALL" is given all store arrays containing objects of type TO are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: A vector of relations.

Definition at line 197 of file RelationsObject.h.

    {
      return RelationVector<TO>(DataStore::Instance().getRelationsWith(DataStore::c_ToSide, this, m_cacheDataStoreEntry,
                                m_cacheArrayIndex, TO::Class(), name, namedRelation));
    }

◆ getRelationsWith()

RelationVector< T > getRelationsWith	(	const std::string &	name = `""`,
		const std::string &	namedRelation = `""`
	)		const

inlineinherited

Get the relations between this object and another store array.

Relations in both directions are returned.

Template Parameters

T	The class of objects to or from which the relations point.

Parameters

name	The name of the store array to or from which the relations point. If empty the default store array name for class T will be used. If the special name "ALL" is given all store arrays containing objects of type T are considered.
namedRelation	Additional name for the relation, or "" for the default naming

Returns: A vector of relations.

Definition at line 230 of file RelationsObject.h.

    {
      return RelationVector<T>(DataStore::Instance().getRelationsWith(DataStore::c_BothSides, this, m_cacheDataStoreEntry,
                               m_cacheArrayIndex, T::Class(), name, namedRelation));
    }

◆ getSinPhi0()

double getSinPhi0 ( ) const

inline

Getter for the cosine of the azimuth angle of travel direction at the perigee.

Definition at line 384 of file Helix.h.

384{ return std::sin(getPhi0()); }

◆ getTangentialAtArcLength2D()

ROOT::Math::XYZVector getTangentialAtArcLength2D ( const double & arcLength2D ) const

Calculates the tangential vector to the helix curve at the given two dimensional arc length.

The tangential vector is the derivative of the position with respect to the two dimensional arc length It is normalised such that the cylindrical radius of the result is 1

getTangentialAtArcLength2D(arcLength2D).Perp() == 1 holds.

Parameters

arcLength2D Two dimensional arc length to be traversed.

Returns: Tangential vector normalised to unit transverse component / cylindrical radius.

Definition at line 245 of file Helix.cc.

{
  const double omega = getOmega();
  const double phi0 = getPhi0();
  const double tanLambda = getTanLambda();
 
  const double chi = - omega * arcLength2D;
 
  const double tx = cos(chi + phi0);
  const double ty = sin(chi + phi0);
  const double tz = tanLambda;
 
  ROOT::Math::XYZVector tangential(tx, ty, tz);
  return tangential;
}

◆ getTanLambda()

double getTanLambda ( ) const

inline

Getter for tan lambda, which is the z over two dimensional arc length slope of the track.

Definition at line 393 of file Helix.h.

393{ return m_tanLambda; }

◆ getTransverseMomentum()

double getTransverseMomentum ( const double bZ ) const

Getter for the absolute value of the transverse momentum at the perigee.

Parameters

bZ	Magnetic field at the perigee

Definition at line 99 of file Helix.cc.

{
  return 1 / std::fabs(getAlpha(bZ) * getOmega());
}

◆ getUnitTangentialAtArcLength2D()

ROOT::Math::XYZVector getUnitTangentialAtArcLength2D ( const double & arcLength2D ) const

Calculates the unit tangential vector to the helix curve at the given two dimensional arc length.

Parameters

arcLength2D Two dimensional arc length to be traversed.

Definition at line 261 of file Helix.cc.

{
  ROOT::Math::XYZVector unitTangential = getTangentialAtArcLength2D(arcLength2D);
  const double norm = hypot(1, getTanLambda());
  const double invNorm = 1 / norm;
  unitTangential *= invNorm;
  return unitTangential;
}

◆ getZ0()

double getZ0 ( ) const

inline

Getter for z0, which is the z coordinate of the perigee.

Definition at line 390 of file Helix.h.

390{ return m_z0; }

◆ passiveMoveBy() [1/2]

double passiveMoveBy	(	const double &	byX,
		const double &	byY,
		const double &	byZ
	)

Moves origin of the coordinate system (passive transformation) orthogonal to the z axis by the given vector.

Updates the helix inplace.

Parameters

byX	X displacement by which the origin of the coordinate system should be moved.
byY	Y displacement by which the origin of the coordinate system should be moved.
byZ	Z displacement by which the origin of the coordinate system should be moved.

Returns: The double value is the two dimensional arc length, which has the be traversed from the old perigee to the new.

Update the parameters inplace. Omega and tan lambda are unchanged

Definition at line 279 of file Helix.cc.

{
  // First calculate the distance of the new origin to the helix in the xy projection
  double new_d0 = 0;
  double arcLength2D = 0;
  calcArcLength2DAndDrAtXY(byX, byY, arcLength2D, new_d0);
 
  // Third the new phi0 and z0 can be calculated from the arc length
  double chi = -arcLength2D * getOmega();
  double new_phi0 = m_phi0 + chi;
  double new_z0 = getZ0() - byZ + getTanLambda() * arcLength2D;
 
  m_d0 = new_d0;
  m_phi0 = new_phi0;
  m_z0 = new_z0;
 
  return arcLength2D;
}

◆ passiveMoveBy() [2/2]

double passiveMoveBy ( const ROOT::Math::XYZVector & by )

inline

Moves origin of the coordinate system (passive transformation) by the given vector.

Updates the helix inplace.

Parameters

by	Vector by which the origin of the coordinate system should be moved.

Returns: The double value is the two dimensional arc length, which has the be traversed from the old perigee to the new.

Definition at line 245 of file Helix.h.

246 { return passiveMoveBy(by.X(), by.Y(), by.Z()); }

Belle2::Helix::passiveMoveBy

double passiveMoveBy(const ROOT::Math::XYZVector &by)

Moves origin of the coordinate system (passive transformation) by the given vector.

Definition: Helix.h:245

◆ reverse()

void reverse ( )

Reverses the direction of travel of the helix in place.

The same points that are located on the helix stay are the same after the transformation, but have the opposite two dimensional arc length associated to them. The momentum at each point is reversed. The charge sign is changed to its opposite by this transformation.

Definition at line 119 of file Helix.cc.

{
  // All except z0 have to be taken to their opposites
  m_d0 = -m_d0; //d0
  m_phi0 = reversePhi(m_phi0);
  m_omega = -m_omega;
  m_tanLambda = -m_tanLambda;
}

◆ reversePhi()

double reversePhi ( const double & phi )

static

Reverses an azimuthal angle to the opposite direction.

Parameters

phi	A angle in [-pi, pi]

Returns: The angle for the opposite direction in [-pi, pi]

Definition at line 421 of file Helix.cc.

{
  return std::remainder(phi + M_PI, 2 * M_PI);
}

◆ setCartesian()

void setCartesian	(	const ROOT::Math::XYZVector &	position,
		const ROOT::Math::XYZVector &	momentum,
		const short int	charge,
		const double	bZ
	)

private

Cartesian to Perigee conversion.

Definition at line 588 of file Helix.cc.

{
  assert(abs(charge) <= 1);  // Not prepared for doubly-charged particles.
  const double alpha = getAlpha(bZ);
 
  // We allow for the case that position, momentum are not given
  // exactly in the perigee.  Therefore we have to transform the momentum
  // with the position as the reference point and then move the coordinate system
  // to the origin.
 
  const double x = position.X();
  const double y = position.Y();
  const double z = position.Z();
 
  const double px = momentum.X();
  const double py = momentum.Y();
  const double pz = momentum.Z();
 
  const double ptinv = 1 / hypot(px, py);
  const double omega = charge * ptinv / alpha;
  const double tanLambda = ptinv * pz;
  const double phi0 = atan2(py, px);
  const double z0 = z;
  const double d0 = 0;
 
  m_omega = omega;
  m_phi0 = phi0;
  m_d0 = d0;
  m_tanLambda = tanLambda;
  m_z0 = z0;
 
  passiveMoveBy(-x, -y, 0);
}

Friends And Related Function Documentation

◆ operator<<

std::ostream & operator<<	(	std::ostream &	output,
		const Helix &	helix
	)

friend

Output operator for debugging and the generation of unittest error messages.

Definition at line 631 of file Helix.cc.

  {
    return output
           << "Helix("
           << "d0=" << helix.getD0() << ", "
           << "phi0=" << helix.getPhi0() << ", "
           << "omega=" << helix.getOmega() << ", "
           << "z0=" << helix.getZ0() << ", "
           << "tanLambda=" << helix.getTanLambda() << ")";
  }

Member Data Documentation

◆ m_cacheArrayIndex

int m_cacheArrayIndex

mutableprivateinherited

Cache of the index in the TClonesArray to which this object belongs.

Definition at line 432 of file RelationsObject.h.

◆ m_cacheDataStoreEntry

DataStore::StoreEntry* m_cacheDataStoreEntry

mutableprivateinherited

Cache of the data store entry to which this object belongs.

Definition at line 429 of file RelationsObject.h.

◆ m_d0

Double32_t m_d0

private

Memory for the signed distance to the perigee.

The sign is the same as of the z component of getPerigee().Cross(getMomentum()).

Definition at line 414 of file Helix.h.

◆ m_omega

Double32_t m_omega

private

Memory for the curvature of the signed curvature.

Definition at line 420 of file Helix.h.

◆ m_phi0

Double32_t m_phi0

private

Memory for the azimuth angle between the transverse momentum and the x axis, which is in [-pi, pi].

Definition at line 417 of file Helix.h.

◆ m_tanLambda

Double32_t m_tanLambda

private

Memory for the slope of the track in the z coordinate over the two dimensional arc length (dz/ds)

Definition at line 426 of file Helix.h.

◆ m_z0

Double32_t m_z0

private

Memory for the z coordinate of the perigee.

Definition at line 423 of file Helix.h.

The documentation for this class was generated from the following files:

framework/dataobjects/include/Helix.h
framework/dataobjects/src/Helix.cc

Public Member Functions

Protected Member Functions

Static Protected Member Functions

Private Member Functions

Private Attributes

Friends

Getters for cartesian parameters of the perigee

Simple extrapolations of the ideal helix

Detailed Description

Constructor & Destructor Documentation

◆ Helix() [1/3]

◆ Helix() [2/3]

◆ Helix() [3/3]

Member Function Documentation

◆ addRelationTo() [1/2]

◆ addRelationTo() [2/2]

◆ calcArcLength2DAndDrAtXY()

◆ calcArcLength2DAtDeltaCylindricalRAndDr()

◆ calcArcLength2DFromSecantLength()

◆ calcASinXDividedByX()

◆ calcATanXDividedByX()

◆ calcDerivativeOfATanXDividedByX()

◆ calcPassiveMoveByJacobian() [1/2]

◆ calcPassiveMoveByJacobian() [2/2]

◆ calcSecantLengthToArcLength2DFactor()

◆ copyRelations()

◆ getAlpha()

◆ getArcLength2DAtCylindricalR()

◆ getArcLength2DAtNormalPlane()

◆ getArcLength2DAtXY()

◆ getArrayIndex()

◆ getArrayName()

◆ getArrayPointer()

◆ getChargeSign()

◆ getCosPhi0()

◆ getCotTheta()

◆ getD0()

◆ getDirection()

◆ getInfo()

◆ getInfoHTML()

◆ getKappa()

◆ getMomentum()

◆ getMomentumAtArcLength2D()

◆ getMomentumX()

◆ getMomentumY()

◆ getMomentumZ()

◆ getName()

◆ getOmega()

◆ getPerigee()

◆ getPerigeeX()

◆ getPerigeeY()

◆ getPerigeeZ()

◆ getPhi0()

◆ getPositionAtArcLength2D()

◆ getRelated()

◆ getRelatedFrom()

◆ getRelatedFromWithWeight()

◆ getRelatedTo()

◆ getRelatedToWithWeight()

◆ getRelatedWithWeight()

◆ getRelationsFrom()

◆ getRelationsTo()

◆ getRelationsWith()

◆ getSinPhi0()

◆ getTangentialAtArcLength2D()

◆ getTanLambda()

◆ getTransverseMomentum()

◆ getUnitTangentialAtArcLength2D()

◆ getZ0()

◆ passiveMoveBy() [1/2]

◆ passiveMoveBy() [2/2]

◆ reverse()

◆ reversePhi()

◆ setCartesian()

Friends And Related Function Documentation

◆ operator<<

Member Data Documentation

◆ m_cacheArrayIndex

◆ m_cacheDataStoreEntry

◆ m_d0