Helix parameter class. More...

#include <Helix.h>

Inheritance diagram for Helix:

Collaboration diagram for Helix:

[legend]

Public Member Functions
	Helix (const HepPoint3D &pivot, const HepVector &a, const HepSymMatrix &Ea)
	Constructor with pivot, helix parameter a, and its error matrix.

	Helix (const HepPoint3D &pivot, const HepVector &a)
	Constructor without error matrix.

	Helix (const HepPoint3D &position, const Hep3Vector &momentum, double charge)
	Constructor with position, momentum, and charge.

virtual	~Helix ()
	Destructor.

const HepPoint3D &	center (void) const
	returns position of helix center(z = 0.);

const HepPoint3D &	pivot (void) const
	returns pivot position.

double	radius (void) const
	returns radious of helix.

HepPoint3D	x (double dPhi=0.) const
	returns position after rotating angle dPhi in phi direction. More...

double *	x (double dPhi, double p[3]) const
	returns position after rotating angle dPhi in phi direction. More...

HepPoint3D	x (double dPhi, HepSymMatrix &Ex) const
	returns position and convariance matrix(Ex) after rotation.

Hep3Vector	direction (double dPhi=0.) const
	returns direction vector after rotating angle dPhi in phi direction.

Hep3Vector	momentum (double dPhi=0.) const
	returns momentum vector after rotating angle dPhi in phi direction.

Hep3Vector	momentum (double dPhi, HepSymMatrix &Em) const
	returns momentum vector after rotating angle dPhi in phi direction.

HepLorentzVector	momentum (double dPhi, double mass) const
	returns 4momentum vector after rotating angle dPhi in phi direction.

HepLorentzVector	momentum (double dPhi, double mass, HepSymMatrix &Em) const
	returns 4momentum vector after rotating angle dPhi in phi direction.

HepLorentzVector	momentum (double dPhi, double mass, HepPoint3D &x, HepSymMatrix &Emx) const
	returns 4momentum vector after rotating angle dPhi in phi direction.

double	dr (void) const
	Return helix parameter dr.

double	phi0 (void) const
	Return helix parameter phi0.

double	kappa (void) const
	Return helix parameter kappa.

double	dz (void) const
	Return helix parameter dz.

double	tanl (void) const
	Return helix parameter tangent lambda.

double	curv (void) const
	Return curvature of helix.

double	sinPhi0 (void) const
	Return sin phi0.

double	cosPhi0 (void) const
	Return cos phi0.

const HepVector &	a (void) const
	Returns helix parameters.

const HepSymMatrix &	Ea (void) const
	Returns error matrix.

const HepVector &	a (const HepVector &newA)
	Sets helix parameters.

const HepSymMatrix &	Ea (const HepSymMatrix &newdA)
	Sets helix paramters and error matrix.

const HepPoint3D &	pivot (const HepPoint3D &newPivot)
	Sets pivot position.

void	set (const HepPoint3D &pivot, const HepVector &a, const HepSymMatrix &Ea)
	Sets helix pivot position, parameters, and error matrix.

void	ignoreErrorMatrix (void)
	Unsets error matrix. More...

double	bFieldZ (double bz)
	Sets/returns z componet of the magnetic field. More...

double	bFieldZ (void) const
	Returns z componet of the magnetic field.

Helix &	operator= (const Helix &)
	Copy operator.

HepMatrix	delApDelA (const HepVector &ap) const
	DAp/DA.

HepMatrix	delXDelA (double phi) const
	DX/DA.

HepMatrix	delMDelA (double phi) const
	DM/DA.

HepMatrix	del4MDelA (double phi, double mass) const
	DM4/DA.

HepMatrix	del4MXDelA (double phi, double mass) const
	DMX4/DA.

Static Public Member Functions
static void	set_limits (const HepVector &a_min, const HepVector &a_max)
	set limit for parameter "a"

static bool	set_exception (bool)
	set exception

static bool	set_print (bool)
	Set print option for debugging.

Static Public Attributes
static const double	ConstantAlpha = 222.376063
	Constant alpha for uniform field.

Private Member Functions
void	updateCache (void)
	updateCache

void	checkValid (void)
	Check whether helix parameters is valid or not. More...

void	debugPrint (void) const
	Print the helix parameters to stdout.

void	debugHelix (void) const
	Debug Helix.

Private Attributes
bool	m_matrixValid
	True: matrix valid, False: matrix not valid.

bool	m_helixValid
	True: helix valid, False: helix not valid.

double	m_bField
	Magnetic field, assuming uniform Bz in the unit of kG.

double	m_alpha
	10000.0/(speed of light)/B.

HepPoint3D	m_pivot
	Pivot.

HepVector	m_a
	Helix parameter.

HepSymMatrix	m_Ea
	Error of the helix parameter.

HepPoint3D	m_center
	Cache of the center position of Helix.

double	m_cp
	Cache of the cos phi0.

double	m_sp
	Cache of the sin phi0.

double	m_pt
	Cache of the pt.

double	m_r
	Cache of the r.

double	m_ac [5]
	Cache of the helix parameter.

Static Private Attributes
static HepVector	ms_amin
	minimum limit of Helix parameter a

static HepVector	ms_amax
	maxiimum limit of Helix parameter a

static bool	ms_check_range
	Check the helix parameter's range.

static bool	ms_print_debug
	Debug option flag.

static bool	ms_throw_exception
	Throw exception flag.

static const std::string	invalidhelix
	String "Invalid Helix".

Detailed Description

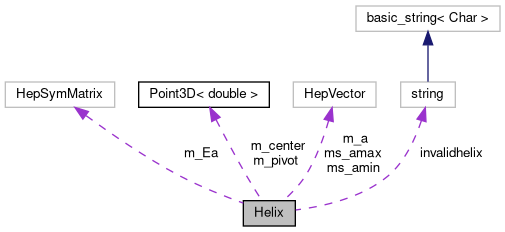
Helix parameter class.

Definition at line 48 of file Helix.h.

Member Function Documentation

◆ bFieldZ()

double bFieldZ ( double bz )

inline

Sets/returns z componet of the magnetic field.

Parameters

[in] bz z-component of the magnetic field.

Attention: Helix param. alpha is also stored.

Definition at line 473 of file Helix.h.

◆ checkValid()

void checkValid ( void )

private

Check whether helix parameters is valid or not.

Sets m_helixValid.

Definition at line 895 of file Helix.cc.

◆ ignoreErrorMatrix()

void ignoreErrorMatrix ( void )

Unsets error matrix.

Error calculations will be ignored after this function call until an error matrix be set again. 0 matrix will be return as a return value for error matrix when you call functions which returns an error matrix.

Definition at line 872 of file Helix.cc.

◆ x() [1/2]

double * x	(	double	dPhi,
		double	p[3]
	)		const

returns position after rotating angle dPhi in phi direction.

x = x0 + dr * cos(phi0) + (alpha / kappa) * (cos(phi0) - cos(phi0+phi)) y = y0 + dr * sin(phi0) + (alpha / kappa) * (sin(phi0) - sin(phi0+phi)) z = z0 + dz - (alpha / kappa) * tan(lambda) * phi

Returns: double[3]

Definition at line 216 of file Helix.cc.

◆ x() [2/2]

HepPoint3D x ( double dPhi = 0. ) const

returns position after rotating angle dPhi in phi direction.

x = x0 + dr * cos(phi0) + (alpha / kappa) * (cos(phi0) - cos(phi0+phi)) y = y0 + dr * sin(phi0) + (alpha / kappa) * (sin(phi0) - sin(phi0+phi)) z = z0 + dz - (alpha / kappa) * tan(lambda) * phi

Returns: HepPoint3D

Definition at line 197 of file Helix.cc.

The documentation for this class was generated from the following files:

cdc/simulation/include/Helix.h
cdc/simulation/src/Helix.cc

Public Member Functions

Static Public Member Functions

Static Public Attributes

Private Member Functions

Private Attributes