FoxWolfram Class Reference

Class to calculate the Fox-Wolfram moments up to order 8. More...

#include <FoxWolfram.h>

Collaboration diagram for FoxWolfram:

Public Member Functions
	FoxWolfram ()
	Default constructor.
	FoxWolfram (const std::vector< ROOT::Math::XYZVector > &momenta)
	Constructor with an array of 3-momenta.
	~FoxWolfram ()
	Default destructor.
void	calculateBasicMoments ()
	Method to perform the calculation of the moments up to order 4, which are the most relevant ones. More...
void	calculateAllMoments ()
	Method to perform the calculation of the moments up to order 8. More...
void	setMomenta (const std::vector< ROOT::Math::XYZVector > &momenta)
	Sets the list of momenta used for the FW moment calculation, overwriting whatever list has been set before.
double	getH (int i) const
	Returns the i-th moment.
double	getR (int i) const
	Returns the i-th moment normalized to the 0th-order moment. More...

Private Attributes
double	m_moment [9] = {0.}
	The moments.
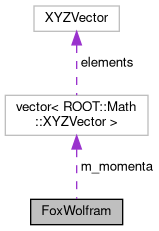
std::vector< ROOT::Math::XYZVector >	m_momenta
	The particle's momenta.

Detailed Description

Class to calculate the Fox-Wolfram moments up to order 8.

Since the most common user case is the calculation of the moments up to order 4, and the calculation of the momenta 5-8 takes much longer, two methods have been implemented. FoxWolfram::calculateBasicMoments will calculate the moments up to 4, while FoxWolfram::calculateAllMoments will perform the calculation up to order 8. The two options have been implemented in two separate methods instead of using an if condition simply to minimize the computing time.

Definition at line 28 of file FoxWolfram.h.

Member Function Documentation

calculateAllMoments()

void calculateAllMoments

(

)

Method to perform the calculation of the moments up to order 8.

It adds a significant overhead to the total FW moments calculation time, so it should be used for debugging or development studies.

Definition at line 58 of file FoxWolfram.cc.

{
  // clear the momenta, in case someone calls this function twice
  for (double& i : m_moment)
    i = 0.;
 
  const auto begin = m_momenta.begin();
  const auto end = m_momenta.end();
 
  // loops over the vector pairs
  for (auto iter1 = begin; iter1 != end; iter1++) {
    const XYZVector pVec1 = (*iter1);
    double pMag1 = pVec1.R();
 
    // avoids to iterate twice over the same pairs
    for (auto iter2 = iter1; iter2 != end; iter2++) {
      const XYZVector pVec2 = (*iter2);
      double magProd = pMag1 * pVec2.R();  // product of the vector's magnitudes
      double cTheta = pVec1.Dot(pVec2) / magProd; // costheta_ij
 
      // Since the FW moment definition requires to double count all the
      // pairs of different particles,  but the smart loop implemented here doesn't,
      // multiply each entry by 2.
      if (iter1 != iter2) magProd *= 2;
 
      // Fills the moments' list.
      // This part is quite ugly, but hard-coding the Legendre polynomials makes the code
      // much faster than using the boost libraries, which are implementing the recursive formulas.
      // This implementation should also be faster than a switch...case one.
      double cTheta2 = cTheta * cTheta;
      double cTheta3 = cTheta2 * cTheta;
      double cTheta4 = cTheta2 * cTheta2;
      double cTheta5 = cTheta4 * cTheta;
      double cTheta6 = cTheta3 * cTheta3;
      double cTheta7 = cTheta6 * cTheta;
      double cTheta8 = cTheta4 * cTheta4;
 
      m_moment[0] += magProd;
      m_moment[1] += magProd * cTheta;
      m_moment[2] += magProd * 0.5 * (3.*cTheta2 - 1);
      m_moment[3] += magProd * 0.5 * (5.*cTheta3 - 3.*cTheta);
      m_moment[4] += magProd * 0.125 * (35.*cTheta4 - 30.*cTheta2 + 3.);
      m_moment[5] += magProd * 0.125 * (63.*cTheta5 - 70 * cTheta3 + 15.*cTheta);
      m_moment[6] += magProd * 0.0625 * (231.*cTheta6 - 315 * cTheta4 + 105 * cTheta2 - 5.);
      m_moment[7] += magProd * 0.0625 * (429.*cTheta7 - 693.*cTheta5 + 315.*cTheta3 - 35.*cTheta);
      m_moment[8] += magProd * 0.0078125 * (6435.*cTheta8 - 12012.*cTheta6 + 6930.*cTheta4 - 1260.*cTheta2 + 35.);
    }
  }
  return;
}

calculateBasicMoments()

void calculateBasicMoments

(

)

Method to perform the calculation of the moments up to order 4, which are the most relevant ones.

The momenta up to order 8 can be calculated calling FoxWolfram::calculateAllMoments().

Definition at line 14 of file FoxWolfram.cc.

getR()

double getR ( int  i ) const

inline

Returns the i-th moment normalized to the 0th-order moment.

These are the quantites normally used for the event shape characterization and the continuum suppression.

Definition at line 89 of file FoxWolfram.h.

{ return (i < 0 || i > 8 || m_moment[0] == 0) ? NAN : m_moment[i] / m_moment[0]; }

---

The documentation for this class was generated from the following files:

• analysis/ContinuumSuppression/include/FoxWolfram.h
• analysis/ContinuumSuppression/src/FoxWolfram.cc