7.7. Truth-matching#

7.7.1. MC matching#

A general overview of the main MC matching algorithm and its user interface can be found in the proceeding Monte Carlo matching in the Belle II software for the CHEP 2021 conference.

First, you must run it#

MCMatching relates Particle and MCParticle objects.

Important

Most MC matching variables will have non-trivial values only if the MCMatcherParticles module is actually executed. It can be executed by adding the module to your path, there is a modularAnalysis.matchMCTruth convenience function to do this.

Core#

MC matching at Belle II returns two important pieces of information: the true PDG id of the particle mcPDG, and an error flag mcErrors.

Both variables will have non-trivial values only if the MCMatching module, which relates composite Particle (s) and MCParticle (s), is executed. mcPDG is set to the PDG code of the first common mother MCParticle of the daughters of this Particle.

mcErrors

The bit pattern indicating the quality of MC match (see MCMatching::MCErrorFlags)

Group: MC matching and MC truth

mcPDG

The PDG code of matched MCParticle, NaN if no match. Requires running matchMCTruth() on the reconstructed particles, or a particle list filled with generator particles (MCParticle objects).

Group: MC matching and MC truth

Extra variables#

There are several extra variables relating to MCMatching. Many are defined for convenience and can be recreated logically from mcPDG and mcErrors. Some extra variables are provided externally, for example isCloneTrack from the tracking-level MC matching.

genNMissingDaughter(PDG)

Returns the number of missing daughters having assigned PDG codes. NaN if no MCParticle is associated to the particle.

Group: MC matching and MC truth

genNStepsToDaughter(i)

Returns number of steps to i-th daughter from the particle at generator level. NaN if no MCParticle is associated to the particle or i-th daughter. NaN if i-th daughter does not exist.

Group: MC matching and MC truth

isCloneTrack

Return 1 if the charged final state particle comes from a cloned track, 0 if not a clone. Returns NAN if neutral, composite, or MCParticle not found (like for data or if not MCMatched)

Group: MC matching and MC truth

isMisidentified

Return 1 if the particle is misidentified: at least one of the final state particles has the wrong PDG code assignment (including wrong charge), 0 if PDG code is fine, and NaN if no related MCParticle could be found.

Group: MC matching and MC truth

isOrHasCloneTrack

Return 1 if the particle is a clone track or has a clone track as a daughter, 0 otherwise.

Group: MC matching and MC truth

isSignal

1.0 if Particle is correctly reconstructed (SIGNAL), 0.0 if not, and NaN if no related MCParticle could be found. It behaves according to DecayStringGrammar.

Group: MC matching and MC truth

isSignalAcceptMissing

Same as isSignal, but also accept missing particle

Group: MC matching and MC truth

isSignalAcceptMissingGamma

Same as isSignal, but also accept missing gamma, such as B -> K* gamma, pi0 -> gamma gamma

Group: MC matching and MC truth

isSignalAcceptMissingMassive

Same as isSignal, but also accept missing massive particle

Group: MC matching and MC truth

isSignalAcceptMissingNeutrino

Same as isSignal, but also accept missing neutrino

Group: MC matching and MC truth

isSignalAcceptWrongFSPs

1.0 if Particle is almost correctly reconstructed (SIGNAL), 0.0 if not, and NaN if no related MCParticle could be found. Misidentification of charged FSP is allowed.

Group: MC matching and MC truth

isWrongCharge

Return 1 if the charge of the particle is wrongly assigned, 0 if it’s the correct charge, and NaN if no related MCParticle could be found.

Group: MC matching and MC truth

Error flags#

The error flag mcErrors is a bit set where each bit flag describes a different kind of discrepancy between reconstruction and MCParticle. The individual flags are described by the MCMatching::MCErrorFlags enum. A value of mcErrors equal to 0 indicates perfect reconstruction (signal). Usually candidates with only FSR photons missing are also considered as signal, so you might want to ignore the corresponding c_MissFSR flag. The same is true for c_MissingResonance, which is set for any missing composite particle (e.g. \(K_1\), but also \(D^{*0}\)).

The behavior of mcErrors can be configured by decay string grammar with modularAnalysis.reconstructDecay(). For more information and examples how to use the decay strings correctly, please see DecayString and Grammar for custom MCMatching.

Full documentation of the MCMatching algorithm is described in BELLE2-CONF-PROC-2022-004.

Flag	Explanation
c_Correct = 0	This Particle and all its daughters are perfectly reconstructed.
c_MissFSR = 1	A Final State Radiation (FSR) photon is not reconstructed (based on MCParticle: :c_IsFSRPhoton).
c_MissingResonance = 2	The associated MCParticle decay contained additional non-final-state particles (e.g. a rho) that weren’t reconstructed. This is probably O.K. in most cases.
c_DecayInFlight = 4	A Particle was reconstructed from the secondary decay product of the actual particle. This means that a wrong hypothesis was used to reconstruct it, which e.g. for tracks might mean a pion hypothesis was used for a secondary electron.
c_MissNeutrino = 8	A neutrino is missing (not reconstructed).
c_MissGamma = 16	A photon (not FSR) is missing (not reconstructed).
c_MissMassiveParticle = 32	A generated massive FSP is missing (not reconstructed).
c_MissKlong = 64	A Klong is missing (not reconstructed).
c_MisID = 128	One of the charged final state particles is mis-identified (wrong signed PDG code).
c_AddedWrongParticle = 256	A non-FSP Particle has wrong PDG code, meaning one of the daughters (or their daughters) belongs to another Particle.
c_InternalError = 512	No valid match was found. For tracks, it indicates that there is not a true track related to the reconstructed one. Might indicate fake or background track or cluster.
c_MissPHOTOS = 1024	A photon created by PHOTOS was not reconstructed (based on MCParticle: :c_IsPHOTOSPhoton).
c_AddedRecoBremsPhoton = 2048	A photon added with the bremsstrahlung recovery tools (correctBrems or correctBremsBelle) has no MC particle assigned, or it doesn’t belong to the decay chain of the corrected lepton mother

Example of use#

The two variables together allow the user not only to distinguish signal (correctly reconstructed) and background (incorrectly reconstructed) candidates, but also to study and identify various types of physics background (e.g. mis-ID, partly reconstructed decays, …). To select candidates that have a certain flag set, you can use bitwise and to select only this flag from mcErrors and check if this value is non-zero: (mcErrors & MCMatching::c_MisID) != 0 . For use in a TTree selector, you’ll need to use the integer value of the flag instead:

ntuple->Draw("M", "(mcErrors & 128) != 0")

You can also make use of MCMatching::explainFlags() which prints a human-readable list of flags present in a given bitset. Can also be used in both C++ and python:

import basf2
from ROOT import Belle2, gInterpreter
gInterpreter.ProcessLine('#include "analysis/utility/MCMatching.h"')
print(Belle2.MCMatching.explainFlags(a_weird_mcError_number))

If instead only binary decision (1 = signal, 0 = background) is needed, then for convenience one can use isSignal (or isSignalAcceptMissingNeutrino for semileptonic decays).

from modularAnalysis import variablesToNtuple
variablesToNtuple("X:mycandidates -> Y Z", variables = ["isSignal"] + other_interesting_variables)

assuming you have reconstructed X -> Y Z :

from modularAnalysis import applyCuts
applyCuts('X:myCandidates', 'isSignal==1')

7.7.2. MC decay finder module `ParticleCombinerFromMC`#

Analysis module to reconstruct a given decay using the list of generated particles MCParticle. Only signal particles with isSignal equal to 1 are stored.

The module can be used for:

Determination of the number of generated decays for efficiency studies, especially in the case of inclusive decays (e.g.: What’s the generated number of \(B \to D^0 X\) decays?).
Matched MC decays as input for a truth matching module.

import basf2

# Create main path
main = basf2.create_path()

# Modules to generate events, etc.
...

import modularAnalysis as ma

# Load particles from MCParticle at first
ma.fillParticleListFromMC('K+:MC',    '', path=main)
ma.fillParticleListFromMC('pi+:MC',   '', path=main)
ma.fillParticleListFromMC('e+:MC',    '', path=main)
ma.fillParticleListFromMC('nu_e:MC',  '', path=main)
ma.fillParticleListFromMC('gamma:MC', '', path=main)

"""
Example 1
Search for B+ decaying to anti-D0* e+ nu_e, where anti-D0* decays to [anti-D0 -> K+ pi- pi0] and pi0.
Additional photons emitted are ignored. Charge conjugated decays are matched, too.
"""
# Reconstruct pi0 from gamma gamma at fist for convenience. Then reconstruct B+ with pi0:gg.
ma.reconstructMCDecay('pi0:gg =direct=> gamma:MC gamma:MC', '', path=main)
ma.reconstructMCDecay(
  'B+:DstENu =direct=> [anti-D*0:D0pi0 =direct=> [anti-D0:Kpipi0 =direct=> K+:MC pi-:MC pi0:gg] pi0:gg ] e+:MC nu_e:MC ',
  '',
  path=main)

# One can directly reconstruct pi0:gg in same decay string.
# But in this case, one have to write sub-decay of pi0:gg only once. Otherwise same particles are registered twice.
# ma.reconstructMCDecay(
#     'B+:DstENu =direct=>\
#      [anti-D*0:D0pi0 =direct=> [anti-D0:Kpipi0 =direct=> K+:MC pi-:MC [pi0:gg =direct=> gamma:MC gamma:MC]] pi0:gg ]\
#      e+:MC nu_e:MC ',
#     '',
#     path=main)


"""
Example 2
Search for B+ decaying to anti-D0 + anything, where the anti-D0 decays to K+ pi-.
Ignore additional photons emitted in the anti-D0 decay. Charge conjugated decays
are matched, too. If there is a match found, save to ParticleList 'B+:testB'
"""
# Reconstruct B+ from [anti-D0 =direct=> K+ pi-] accepting missing daughters
ma.reconstructMCDecay('B+:D0Kpi =direct=> [anti-D0:Kpi =direct=> K+:MC pi-:MC] ... ?gamma ?nu', '', path=main)


...

For more information and examples how to use the decay strings correctly, please see DecayString and Grammar for custom MCMatching.

7.7.3. MC decay finder module `MCDecayFinder`#

Analysis module to search for a given decay in the list of generated particles MCParticle.

The module can be used for:

Determination of the number of generated decays for efficiency studies, especially in the case of inclusive decays (e.g.: What’s the generated number of \(B \to D^0 X\) decays?).
Matched MC decays as input for a truth matching module.

import basf2

# Create main path
main = basf2.create_path()

# Modules to generate events, etc.
...

import modularAnalysis as ma
# Search for B+ decaying to anti-D0 + anything, where the anti-D0 decays to K+ pi-.
# Ignore additional photons emitted in the anti-D0 decay. Charge conjugated decays
# are matched, too. If there is a match found, save to ParticleList 'B+:testB'
ma.findMCDecay('B+:testB', 'B+ =direct=> [anti-D0 =direct=> K+ pi-] ... ?gamma ?nu', path=main)

# Modules which can use the matched decays saved as Particle in the ParticleList 'B+:testB'
...

For more information and examples how to use the decay strings correctly, please see DecayString and Grammar for custom MCMatching.

7.7.4. MC decay string#

Analysis module to search for a generator-level decay string for given particle.

Using decay hashes#

The use of decay hashes is demonstrated in B2A502-WriteOutDecayHash.py and B2A503-ReadDecayHash.py.

B2A502-WriteOutDecayHash.py creates one ROOT file, via modularAnalysis.variablesToNtuple containing the requested variables including the two decay hashes, and a second root file containing the two decay hashes and the full decay string. The decay strings can be related to the candidates that they are associated with by matching up the decay hashes. An example of this using python is shown in B2A503-ReadDecayHash.py.

path.add_module('ParticleMCDecayString', listName='my_particle_list', fileName='my_hashmap.root')

This will produce a file with all of the decay strings in it, along with the decayHash (hashes the MC decay string of the mother particle) and decayHashExtended (hashes the decay string of the mother and daughter particles). The mapping of hashes to full MC decay strings is stored in a ROOT file determined by the fileName parameter.

Then the variables extraInfo(decayHash) and extraInfo(decayHashExtended) are available in the VariableManager.

7.7.5. Generated decay modes#

A tool has been developed which analyzes the array of MC particles and determines the generated decay mode of the event.

A total of 825 \(B^+\) decay modes have been defined:

The first 80 numbers are semi-leptonic decays (\(B^+ \to h l^+ \nu_l\)), e.g.

1001: \(B^+ \to \bar{D^{*0}} e^+ \nu_e\)

1002: \(B^+ \to \bar{D^0} e^+ \nu_e\)

1003: \(B^+ \to \bar{D_1^0} e^+ \nu_e\)

The numbers 1085 to 1092 are radiative decays.

There are 17 \(B^+ \to X l^+ l^-\) decay modes.

The numbers 1113 to 1608 are hadronic charmless decays.

Then there are 70 charmonium decays with \(J/\psi\), \(\Psi(2S)\), \(\eta_c\), etc.

This is followed by decays involving two or one charm meson.

The last 17 decay modes involve baryons.

The same number of \(B^-\) decay modes have been implemented. They have negative tags.

BminusMode#

[Eventbased] It will return the decays mode of B- particles

Group: MCParticle tag variables

BplusMode#

[Eventbased] It will return the decays mode of B+ particles

Group: MCParticle tag variables

The same general structure is used for the 1000 \(B^0\) and \(\bar{B^0}\) modes accessible via the variables

B0Mode#

[Eventbased] It will return the decays mode of B0 particles

Group: MCParticle tag variables

Bbar0Mode#

[Eventbased] It will return the decays mode of anti-B0 particles

Group: MCParticle tag variables

For \(B_s^0\) and \(\bar{B_s^0}\) a total of 264 decay have been defined.

Bs0Mode#

[Eventbased] It will return the decays mode of B_s0 particles

Group: MCParticle tag variables

Bsbar0Mode#

[Eventbased] It will return the decays mode of anti-B_s0 particles

Group: MCParticle tag variables

Besides the B meson decays three \(D^{*\pm}\), 84 \(D_s^\pm\), 84 \(D^\pm\), and 136 \(D^0\) charm meson decays are implemented. For each category the tag number starts again at 1001.

D0Mode#

[Eventbased] It will return the decays mode of D0 particles

Group: MCParticle tag variables

Dbar0Mode#

[Eventbased] It will return the decays mode of anti-D0 particles

Group: MCParticle tag variables

DminusMode#

[Eventbased] It will return the decays mode of D- particles

Group: MCParticle tag variables

DplusMode#

[Eventbased] It will return the decays mode of D+ particles

Group: MCParticle tag variables

DsminusMode#

[Eventbased] It will return the decays mode of D_s- particles

Group: MCParticle tag variables

DsplusMode#

[Eventbased] It will return the decays mode of D_s+ particles

Group: MCParticle tag variables

DstminusMode#

[Eventbased] It will return the decays mode of D*- particles

Group: MCParticle tag variables

DstplusMode#

[Eventbased] It will return the decays mode of D*+ particles

Group: MCParticle tag variables

The full list of all decay modes can be found in the technical Belle note BELLE2-NOTE-TE-2021-002.

7.7.6. Tau decay MC modes#

A special case is the decay of generated tau lepton pairs. For their study, it is useful to call the function labelTauPairMC in the steering file.

from modularAnalysis import labelTauPairMC
labelTauPairMC()

tauMinusMCMode#

[Eventbased] Decay ID for the negative tau lepton in a tau pair generated event.

Group: Generated tau decay information

tauMinusMCProng#

[Eventbased] Prong for the negative tau lepton in a tau pair generated event.

Group: Generated tau decay information

tauPlusMCMode#

[Eventbased] Decay ID for the positive tau lepton in a tau pair generated event.

Group: Generated tau decay information

tauPlusMCProng#

[Eventbased] Prong for the positive tau lepton in a tau pair generated event.

Group: Generated tau decay information

Using MC information, labelTauPairMC identifies if the generated event is a tau pair decay.

The variables tauPlusMCProng and tauMinusMCProng store the prong (number of final state charged particles) coming from each one of the generated tau leptons. If the event is not a tau pair decay, the value in each one of these variables will be 0.

The channel number will be stored in the variables tauPlusMCMode, and tauMinusMCMode (one for the positive and the other for the negative) according to the following table:

MC mode	Decay channel	MC mode	Decay channel
-1	Not a tau pair event	24	\(\tau^- \to \pi^- \omega \pi^0 \nu\)
1	\(\tau^- \to e^- \nu \bar{\nu}\)	25	\(\tau^- \to \pi^- \pi^+ \pi^- \eta \nu\)
2	\(\tau^- \to \mu^- \nu \bar{\nu}\)	26	\(\tau^- \to \pi^- \pi^0 \pi^0 \eta \nu\)
3	\(\tau^- \to \pi^- \nu\)	27	\(\tau^- \to K^- \eta \nu\)
4	\(\tau^- \to \rho^- \nu\)	28	\(\tau^- \to K^{*-} \eta \nu\)
5	\(\tau^- \to a_1^- \nu\)	29	\(\tau^- \to K^- \pi^+ \pi^- \pi^0 \nu\)
6	\(\tau^- \to K^- \nu\)	30	\(\tau^- \to K^- \pi^0 \pi^0 \pi^0 \nu\)
7	\(\tau^- \to K^{*-} \nu\)	31	\(\tau^- \to K^0 \pi^- \pi^+ \pi^- \nu\)
8	\(\tau^- \to \pi^- \pi^+ \pi^- \pi^0 \nu\)	32	\(\tau^- \to \pi^- \bar{K}^0 \pi^0 \pi^0 \nu\)
9	\(\tau^- \to \pi^- \pi^0 \pi^0 \pi^0 \nu\)	33	\(\tau^- \to \pi^- K^+ K^- \pi^0 \nu\)
10	\(\tau^- \to 2\pi^- \pi^+ 2\pi^0 \nu\)	34	\(\tau^- \to \pi^- K^0 \bar{K}^0 \pi^0 \nu\)
11	\(\tau^- \to 3\pi^- 2\pi^+ \nu\)	35	\(\tau^- \to \pi^- \omega \pi^+ \pi^- \nu\)
12	\(\tau^- \to 3\pi^- 2\pi^+ \pi^0 \nu\)	36	\(\tau^- \to \pi^- \omega \pi^0 \pi^0 \nu\)
13	\(\tau^- \to 2\pi^- \pi^+ 3\pi^0 \nu\)	37	\(\tau^- \to e^- e^- e^+ \nu \bar{\nu}\)
14	\(\tau^- \to K^- \pi^- K^+ \nu\)	38	\(\tau^- \to f_1 \pi^- \nu\)
15	\(\tau^- \to K^0 \pi^- K^0bar \nu\)	39	\(\tau^- \to K^- \omega \nu\)
16	\(\tau^- \to K^- K^0 \pi^0 \nu\)	40	\(\tau^- \to K^- K^0 \pi^+ \pi^- \nu\)
17	\(\tau^- \to K^- \pi^0 \pi^0 \nu\)	41	\(\tau^- \to K^- K^0 \pi^0 \pi^0 \nu\)
18	\(\tau^- \to K^- \pi^- \pi^+ \nu\)	42	\(\tau^- \to \pi^- K^+ \bar{K}^0 \pi^- \nu\)
19	\(\tau^- \to \pi^- \bar{K}^0 \pi^0 \nu\)
20	\(\tau^- \to \eta \pi^- \pi^0 \nu\)
21	\(\tau^- \to \pi^- \pi^0 \gamma \nu\)
22	\(\tau^- \to K^- K^0 \nu\)
23	\(\tau^- \to \pi^- 4\pi^0 \nu\)

7.7.7. Track matching#

A reconstructed track can be:

matched, the reconstructed track is matched to a true track and it is its best description.
clone, the reconstructed track is matched to a true track, but there is another reconstructed track that better describes the true track (this second reconstructed track will therefore be matched)
fake, the reconstructed track is not matched to any true track. It can be a beam-background track or a track built out of noise hits in the detector, or a mixture of these two.

Note

In case of matched or clone tracks, the charge of the reconstructed track is not checked against the charge of the true track. The charge check is anyway included in the MCMatching that sets the Error flags.

More details on the track matching can be found in the Track Matching section of the Tracking chapter, in particular Reconstructed Track MC-Matching. Here is a table to translate the matching status at tracking level with the one at analysis level:

tracking-level	analysis-level
matched	matched
wrongCharge	matched
clone	clone
cloneWrongCharge	clone
background	fake
ghost	fake

7.7.8. Photon matching#

To understand the method of photon matching, a basic introduction to the ECL objects used during the reconstruction of simulated data is required.

Starting with ECLSimHits from the GEANT4 simulation, ECLDigits are created and then calibrated to make ECLCalDigit objects which store the energy and time of a single ECL crystal. The ECLCalDigits are then grouped to make ECLShower objects. The shower objects are corrected and calibrated, and used to calculate shower-shape quantities and certain particle likelihoods (these calculations are derived using information stored in subsets of the ECLCalDigits that form the shower). Following this, track matching is performed between reconstructed tracks and shower objects. The last step is the conversion of the ECLShower object into a mdst ECLCluster object which is the highest level ECL reconstruction object.

Each ECLShower object (and by extension each ECLCluster object) holds weighted relations to a maximum of twenty-one ECLCalDigits, with the weights calculated using the fraction of energy each ECLCalDigit contributes to each shower. In addition to this, the ECLCalDigit can itself have a weighted relation to none, one or many MCParticles. This is calculated using the total energy deposited by the MCParticle in each ECLCalDigit. A diagram that visualises these relations is given in Fig. 7.1.

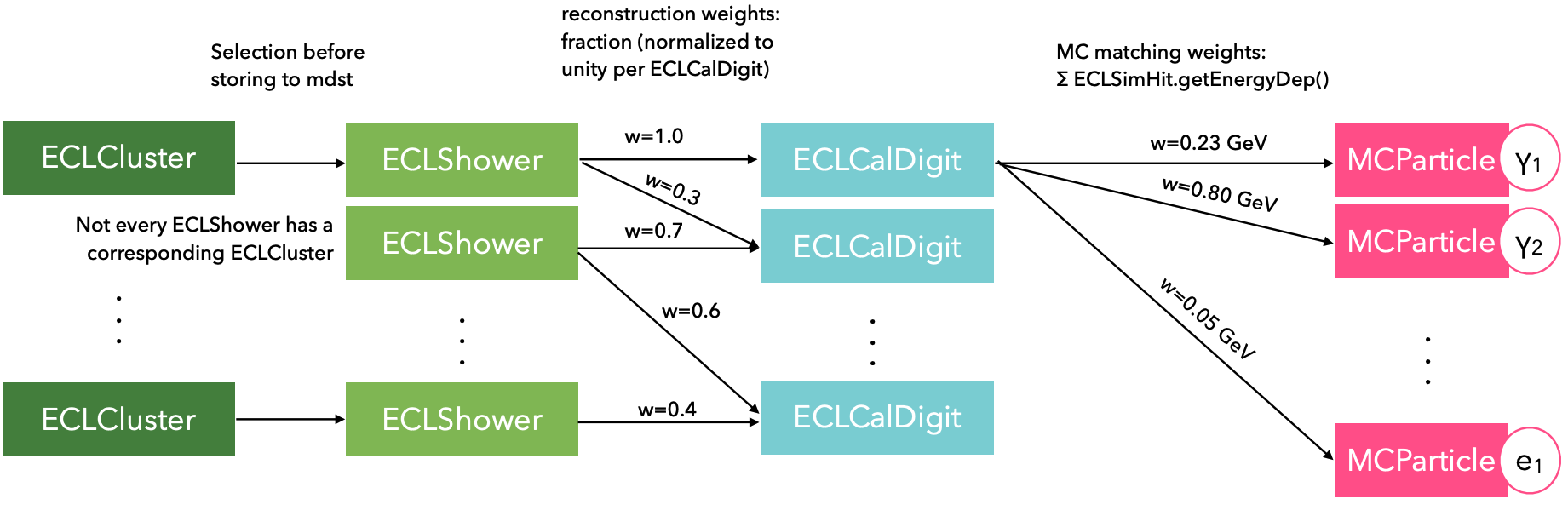
../../_images/photon_matching.png — Fig. 7.1 Schematic diagram showing the weighted relations between ECL reconstruction objects and simulated particles.#

The overall weight for the relation between an ECLCluster object and a MCParticle is then given by the product of the weight between the corresponding ECLShower and ECLCalDigit and the weight between the ECLCalDigit and MCParticle. For example, the weight of the relation between the first ECLCluster in Fig. 7.1 and MCParticle \(\gamma_2\) is given by \(1.0\times 0.8=0.8\) GeV.

An ECLCluster that is not matched to any track is reconstructed as a photon Particle, and relations between the photon Particle and MCParticles are only set at the user-analysis level if the following conditions are met:

\(\mathrm{weight}/{E_\mathrm{rec}} > 0.2\) GeV
\(\mathrm{weight}/{E_\mathrm{true}} > 0.3\) GeV

where the weight here refers to the relation with the largest weight. This means that if multiple relations between a given Particle and MCParticles exist, only the relation with the largest weight will be used, and the corresponding MCParticle with this relation will be used to decide the photon matching.

A photon match is made if mcErrors == 0 and the MCParticle has a mcPDG == 22. If the chosen MCParticle does not correspond to a true photon, then the mcErrors \(\neq\) 0 and no correct match will be made (even if another one of the smaller-weighted relations for the particle is correct).

Information regarding these weights can be accessed on a user-analysis level using the following variables:

Note

These weight variables can be used to help isolate photons that originate from beam background processes. Such photons typically have a very low total weight.

This information has been extracted from this talk. More details about MC matching for photons can be found there and from the references therein.

7.7.9. Topology analysis#

This section provides some information on the interface, repositories, and documents of TopoAna, which is a generic tool for the event type analysis of inclusive MC samples in high energy physics experiments, and hence a powerful tool for analysts to investigate the signals and backgrounds involved in their works. TopoAna is an offline tool independent of basf2. It can take the output root files of the Analysis module as input. The MC truth information for the event type analysis can be stored in the root files with the utility MCGenTopo in basf2. Thus, MCGenTopo is the interface of basf2 to TopoAna.

Note

Apart from the interface, this section only introduces the TopoAna resources outside the Belle II software documentation. Inside the documentation, please see Section 3.5.5 for the online textbook on TopoAna. It is a good idea to start learning the usage of TopoAna with this online textbook. Please feel free to contact Xingyu Zhou (zhouxy@buaa.edu.cn) if you have any questions or comments on TopoAna.

The interface#

As we mention above, MCGenTopo is the interface of basf2 to TopoAna. To be specific, the interface implements the following parameter function mc_gen_topo(n) in the script variables/MCGenTopo.py.

variables.MCGenTopo.mc_gen_topo(n=200)[source]

Gets the list of variables containing the raw topology information of MC generated events. To be specific, the list including the following variables:

nMCGen: number of MC generated particles in a given event,
MCGenPDG_i (i=0, 1, … n-2, n-1): PDG code of the \({\rm i}^{\rm th}\) MC generated particle in a given event,
MCGenMothIndex_i (i=0, 1, … n-2, n-1): mother index of the \({\rm i}^{\rm th}\) MC generated particle in a given event.

Tip

Internally, nMCGen, MCGenPDG_i and MCGenMothIndex_i are just aliases of nMCParticles, genParticle(i, varForMCGen(PDG)) and genParticle(i, varForMCGen(mcMother(mdstIndex))), respectively.
For more details on the variables, please refer to the documentations of nMCParticles, genParticle, varForMCGen, PDG, mcMother, and mdstIndex.

Parameters: n (int) – number of MCGenPDG_i/MCGenMothIndex_i variables. Its default value is 200.

Note

To completely examine the topology information of the events in an MC sample, the parameter n should be greater than or equal to the maximum of nMCGen in the sample.
Normally, the maximum of nMCGen in the MC samples at Belle II is less than 200. Hence, if you have no idea about the maximum of nMCGen in your own MC sample, it is usually a safe choice to use the default parameter value 200.
However, an overlarge parameter value leads to unnecessary waste of disk space and redundant variables with inelegant nan values. Hence, if you know the maximum of nMCGen in your own MC sample, it is a better choice to assign the parameter a proper value.

Below are the steps to use mc_gen_topo(n) to get the input data to TopoAna.

Append the following statement at the beginning part of your python steering script
from variables.MCGenTopo import mc_gen_topo
Use the parameter function mc_gen_topo(n) as a list of variables in the steering function variablesToNtuple as follow
variablesToNtuple(particleList, yourOwnVariableList + mc_gen_topo(n), treeName, fieName, path)
Run your python steering script with basf2

Repositories#

The following three remote repositories of TopoAna are provided at present. The one at Stash is most convenient to Belle II users. Nonetheless, the two at GitHub and at GitLab of IHEP are also provided as helpful alternatives for possible convenience.

Documents#

Use cases at Belle II#

At the end of this section, we list two use cases of TopoAna at Belle II: one for semitauonic analyses and the other for charm analyses. You can refer to them if you work in the related analysis groups.

Using TopoAna with the semitauonic framework by Hannah Marie Wakeling
TopoAna Wrapper for Charm Analysis by Guanda Gong

basf2 release-08-02-02 documentation

Truth-matching

Contents

7.7. Truth-matching#

7.7.1. MC matching#

First, you must run it#

Core#

Extra variables#

Error flags#

Example of use#

7.7.2. MC decay finder module `ParticleCombinerFromMC`#

7.7.3. MC decay finder module `MCDecayFinder`#

7.7.4. MC decay string#

Using decay hashes#

7.7.5. Generated decay modes#

7.7.6. Tau decay MC modes#

7.7.7. Track matching#

7.7.8. Photon matching#

7.7.9. Topology analysis#

The interface#

Repositories#

Documents#

Use cases at Belle II#

basf2 release-08-02-02 documentation

Truth-matching

Contents

7.7. Truth-matching#

7.7.1. MC matching#

First, you must run it#

Core#

Extra variables#

Error flags#

Example of use#

7.7.2. MC decay finder module ParticleCombinerFromMC#

7.7.3. MC decay finder module MCDecayFinder#

7.7.4. MC decay string#

Using decay hashes#

7.7.5. Generated decay modes#

7.7.6. Tau decay MC modes#

7.7.7. Track matching#

7.7.8. Photon matching#

7.7.9. Topology analysis#

The interface#

Repositories#

Documents#

Use cases at Belle II#

7.7.2. MC decay finder module `ParticleCombinerFromMC`#

7.7.3. MC decay finder module `MCDecayFinder`#