SoftGaussMassConstraint Class Reference

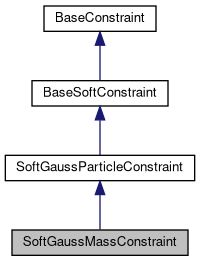
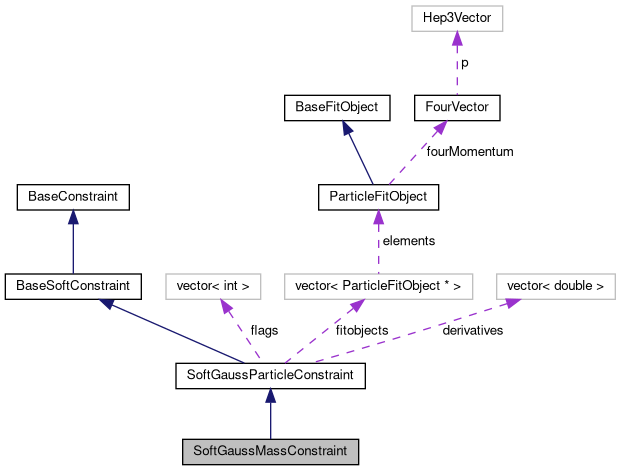
Implements constraint 0 = mass1 - mass2 - m. More...

#include <SoftGaussMassConstraint.h>

Inheritance diagram for SoftGaussMassConstraint:

Collaboration diagram for SoftGaussMassConstraint:

Public Member Functions
	SoftGaussMassConstraint (double sigma_, double mass_=0.)
	Constructor. More...
virtual	~SoftGaussMassConstraint ()
	Virtual destructor.
virtual double	getValue () const override
	Returns the value of the constraint function.
virtual void	getDerivatives (int idim, double der[]) const override
	Get first order derivatives. More...
virtual double	getMass (int flag=1)
	Get the actual invariant mass of the fit objects with a given flag. More...
virtual void	setMass (double mass_)
	Sets the target mass of the constraint. More...
virtual void	setFOList (std::vector< ParticleFitObject * > *fitobjects_)
	Adds several ParticleFitObject objects to the list. More...
virtual void	addToFOList (ParticleFitObject &fitobject, int flag=1)
	Adds one ParticleFitObject objects to the list.
virtual void	resetFOList ()
	Resests ParticleFitObject list.
virtual double	getChi2 () const override
	Returns the chi2.
virtual double	getError () const override
	Returns the error on the value of the constraint.
virtual double	getSigma () const
	Returns the sigma.
virtual double	setSigma (double sigma_)
	Sets the sigma. More...
virtual void	add2ndDerivativesToMatrix (double *M, int idim) const override
	Adds second order derivatives to global covariance matrix M. More...
virtual void	addToGlobalChi2DerVector (double *y, int idim) const override
	Add derivatives of chi squared to global derivative matrix. More...
void	invalidateCache () const
	Invalidates any cached values for the next event.
void	test1stDerivatives ()
void	test2ndDerivatives ()
double	num1stDerivative (int ifo, int ilocal, double eps)
	Evaluates numerically the 1st derivative w.r.t. a parameter. More...
double	num2ndDerivative (int ifo1, int ilocal1, double eps1, int ifo2, int ilocal2, double eps2)
	Evaluates numerically the 2nd derivative w.r.t. 2 parameters. More...
int	getVarBasis () const
virtual const char *	getName () const
	Returns the name of the constraint.
void	setName (const char *name_)
	Set object's name.
virtual std::ostream &	print (std::ostream &os) const
	print object to ostream More...

Protected Types
enum	{ VAR_BASIS = BaseDefs::VARBASIS_EPXYZ }
typedef std::vector< ParticleFitObject * >	FitObjectContainer
	Vector of pointers to ParticleFitObjects.
typedef FitObjectContainer::iterator	FitObjectIterator
	Iterator through vector of pointers to ParticleFitObjects.
typedef FitObjectContainer::const_iterator	ConstFitObjectIterator
	Constant iterator through vector of pointers to ParticleFitObjects.

Protected Member Functions
virtual bool	secondDerivatives (int i, int j, double *derivatives) const override
	Second derivatives with respect to the 4-vectors of Fit objects i and j; result false if all derivatives are zero. More...
virtual bool	firstDerivatives (int i, double *derivatives) const override
	First derivatives with respect to the 4-vector of Fit objects i; result false if all derivatives are zero. More...

Protected Attributes
double	mass
	The mass difference between object sets 1 and 2.
FitObjectContainer	fitobjects
	The FitObjectContainer.
std::vector< double >	derivatives
	The derivatives.
std::vector< int >	flags
	The flags can be used to divide the FitObjectContainer into several subsets used for example to implement an equal mass constraint (see MassConstraint).
double	sigma
	The sigma of the Gaussian.
char *	name

Related Functions
(Note that these are not member functions.)
std::ostream &	operator<< (std::ostream &os, const BaseConstraint &bc)
	Prints out a BaseConstraint, using its print method. More...

Detailed Description

Implements constraint 0 = mass1 - mass2 - m.

This class implements different mass constraints:

• the invariant mass of several objects should be m
• the difference of the invariant masses between two sets of objects should be m (normally m=0 in this case).

Author: Jenny List, Benno List Last update:

Date

2008/02/12 16:43:26

by:

Author

blist

Definition at line 45 of file SoftGaussMassConstraint.h.

Constructor & Destructor Documentation

SoftGaussMassConstraint()

SoftGaussMassConstraint ( double  sigma_, double  mass_ = 0.  )

explicit

Constructor.

Parameters

sigma_	The sigma value
mass_	The mass difference between object sets 1 and 2

Definition at line 35 of file SoftGaussMassConstraint.cc.

      : SoftGaussParticleConstraint(sigma_),
        mass(mass_)
    {}

Member Function Documentation

add2ndDerivativesToMatrix()

void add2ndDerivativesToMatrix ( double *  M, int  idim  ) const

overridevirtualinherited

Adds second order derivatives to global covariance matrix M.

Calculates the second derivative of the constraint g w.r.t.

the various parameters and adds it to the global covariance matrix

We denote with P_i the 4-vector of the i-th ParticleFitObject, then $$ \frac{\partial ^2 g}{\partial a_k \partial a_l} = \sum_i \sum_j \frac{\partial ^2 g}{\partial P_i \partial P_j} \cdot \frac{\partial P_i}{\partial a_k} \cdot \frac{\partial P_j}{\partial a_l}

• \sum_i \frac{\partial g}{\partial P_i} \cdot \frac{\partial^2 P_i}{\partial a_k \partial a_l} $$ Here, $\frac{\partial P_i}{\partial a_k}$ is a $4 \times n_i$ Matrix, where $n_i$ is the number of parameters of FitObject i; Correspondingly, $\frac{\partial^2 P_i}{\partial a_k \partial a_l}$ is a $4 \times n_i \times n_i$ matrix. Also, $\frac{\partial ^2 g}{\partial P_i \partial P_j}$ is a $4\times 4$ matrix for a given i and j, and $\frac{\partial g}{\partial P_i}$ is a 4-vector (though not a Lorentz-vector!).

First, treat the part $$ \frac{\partial ^2 g}{\partial P_i \partial P_j} \cdot \frac{\partial P_i}{\partial a_k} \cdot \frac{\partial P_j}{\partial a_l} $$

Second, treat the parts $$ \sum_i \frac{\partial g}{\partial P_i} \cdot \frac{\partial^2 P_i}{\partial a_k \partial a_l} $$ and $$ \frac{\partial^2 h}{\partial g^2} \sum_i \frac{\partial g}{\partial P_i} \cdot \frac{\partial P_i}{\partial a_k} \sum_j \frac{\partial g}{\partial P_j} \cdot \frac{\partial P_j}{\partial a_l} $$

Here, $\frac{\partial g}{\partial P_i}$ is a 4-vector, which we pass on to the FitObject

Parameters

M	Covariance matrix, at least idim x idim
idim	First dimension of the array

Implements BaseSoftConstraint.

Definition at line 91 of file SoftGaussParticleConstraint.cc.

    {
 
      double s = getSigma();
      double fact = 2 * getValue() / (s * s);
 
      // Derivatives $\frac{\partial ^2 g}{\partial P_i \partial P_j}$ at fixed i, j
      // d2GdPidPj[4*ii+jj] is derivative w.r.t. P_i,ii and P_j,jj, where ii=0,1,2,3 for E,px,py,pz
      double d2GdPidPj[16];
      // Derivatives $\frac {\partial P_i}{\partial a_k}$ for all i;
      // k is local parameter number
      // dPidAk[KMAX*4*i + 4*k + ii] is $\frac {\partial P_{i,ii}}{\partial a_k}$,
      // with ii=0, 1, 2, 3 for E, px, py, pz
      const int KMAX = 4;
      const int n = fitobjects.size();
      auto* dPidAk = new double[n * KMAX * 4];
      bool* dPidAkval = new bool[n];
 
      for (int i = 0; i < n; ++i) dPidAkval[i] = false;
 
      // Derivatives $\frac{\partial ^2 g}{\partial P_i \partial a_l}$ at fixed i
      // d2GdPdAl[4*l + ii] is $\frac{\partial ^2 g}{\partial P_{i,ii} \partial a_l}$
      double d2GdPdAl[4 * KMAX];
      // Derivatives $\frac{\partial ^2 g}{\partial a_k \partial a_l}$
      double d2GdAkdAl[KMAX * KMAX] = {0};
 
      // Global parameter numbers: parglobal[KMAX*i+klocal]
      // is global parameter number of local parameter klocal of i-th Fit object
      int* parglobal = new int[KMAX * n];
 
      for (int i = 0; i < n; ++i) {
        const ParticleFitObject* foi = fitobjects[i];
        assert(foi);
        for (int klocal = 0; klocal < foi->getNPar(); ++klocal) {
          parglobal [KMAX * i + klocal] = foi->getGlobalParNum(klocal);
        }
      }
 
 
      for (int i = 0; i < n; ++i) {
        const ParticleFitObject* foi = fitobjects[i];
        assert(foi);
        for (int j = 0; j < n; ++j) {
          const ParticleFitObject* foj = fitobjects[j];
          assert(foj);
          if (secondDerivatives(i, j, d2GdPidPj)) {
            if (!dPidAkval[i]) {
              foi->getDerivatives(dPidAk + i * (KMAX * 4), KMAX * 4);
              dPidAkval[i] = true;
            }
            if (!dPidAkval[j]) {
              foj->getDerivatives(dPidAk + j * (KMAX * 4), KMAX * 4);
              dPidAkval[j] = true;
            }
            // Now sum over E/px/Py/Pz for object j:
            // $$\frac{\partial ^2 g}{\partial P_{i,ii} \partial a_l}
            //   = (sum_{j}) sum_{jj} frac{\partial ^2 g}{\partial P_{i,ii} \partial P_{j,jj}}
            //     \cdot \frac{\partial P_{j,jj}}{\partial a_l}
            // We're summing over jj here
            for (int llocal = 0; llocal < foj->getNPar(); ++llocal) {
              for (int ii = 0; ii < 4; ++ii) {
                int ind1 = 4 * ii;
                int ind2 = (KMAX * 4) * j + 4 * llocal;
                double& r = d2GdPdAl[4 * llocal + ii];
                r  = d2GdPidPj[  ind1] * dPidAk[  ind2];   // E
                r += d2GdPidPj[++ind1] * dPidAk[++ind2];   // px
                r += d2GdPidPj[++ind1] * dPidAk[++ind2];   // py
                r += d2GdPidPj[++ind1] * dPidAk[++ind2];   // pz
              }
            }
            // Now sum over E/px/Py/Pz for object i, i.e. sum over ii:
            // $$
            // \frac{\partial ^2 g}{\partial a_k \partial a_l}
            //      = \sum_{ii} \frac{\partial ^2 g}{\partial P_{i,ii} \partial a_l} \cdot
            //        \frac{\partial P_{i,ii}}{\partial a_k}
            // $$
            for (int klocal = 0; klocal < foi->getNPar(); ++klocal) {
              for (int llocal = 0; llocal < foj->getNPar(); ++llocal) {
                int ind1 = 4 * llocal;
                int ind2 = (KMAX * 4) * i + 4 * klocal;
                double& r = d2GdAkdAl[KMAX * klocal + llocal];
                r  = d2GdPdAl[  ind1] * dPidAk[  ind2];    //E
                r += d2GdPdAl[++ind1] * dPidAk[++ind2];   // px
                r += d2GdPdAl[++ind1] * dPidAk[++ind2];   // py
                r += d2GdPdAl[++ind1] * dPidAk[++ind2];   // pz
              }
            }
            // Now expand the local parameter numbers to global ones
            for (int klocal = 0; klocal < foi->getNPar(); ++klocal) {
              int kglobal = parglobal [KMAX * i + klocal];
              for (int llocal = 0; llocal < foj->getNPar(); ++llocal) {
                int lglobal = parglobal [KMAX * j + llocal];
                M [idim * kglobal + lglobal] += fact * d2GdAkdAl[KMAX * klocal + llocal];
              }
            }
          }
        }
      }
      auto* v = new double[idim];
      for (int i = 0; i < idim; ++i) v[i] = 0;
      double sqrtfact2 = sqrt(2.0) / s;
 
      double dgdpi[4];
      for (int i = 0; i < n; ++i) {
        const ParticleFitObject* foi = fitobjects[i];
        assert(foi);
        if (firstDerivatives(i, dgdpi)) {
          foi->addTo2ndDerivatives(M, idim, fact, dgdpi, getVarBasis());
          foi->addToGlobalChi2DerVector(v, idim, sqrtfact2, dgdpi, getVarBasis());
        }
      }
 
      for (int i = 0; i < idim; ++i) {
        if (double vi = v[i]) {
          int ioffs = i * idim;
          for (double* pvj = v; pvj < v + idim; ++pvj) {
            M[ioffs++] += vi * (*pvj);
          }
        }
      }
 
 
      delete[] dPidAk;
      delete[] dPidAkval;
      delete[] parglobal;
      delete[] v;
    }

addToGlobalChi2DerVector()

void addToGlobalChi2DerVector ( double *  y, int  idim  ) const

overridevirtualinherited

Add derivatives of chi squared to global derivative matrix.

Parameters

y	Vector of chi2 derivatives
idim	Vector size

Implements BaseSoftConstraint.

Definition at line 243 of file SoftGaussParticleConstraint.cc.

firstDerivatives()

bool firstDerivatives ( int  i, double *  derivatives  ) const

overrideprotectedvirtual

First derivatives with respect to the 4-vector of Fit objects i; result false if all derivatives are zero.

Parameters

i	number of 1st FitObject
derivatives	The result 4-vector

Implements SoftGaussParticleConstraint.

Definition at line 191 of file SoftGaussMassConstraint.cc.

getDerivatives()

void getDerivatives ( int  idim, double  der[]  ) const

overridevirtual

Get first order derivatives.

Call this with a predefined array "der" with the necessary number of entries!

Parameters

idim	First dimension of the array
der	Array of derivatives, at least idim x idim

Implements SoftGaussParticleConstraint.

Definition at line 68 of file SoftGaussMassConstraint.cc.

getMass()

double getMass ( int  flag = 1 )

virtual

Get the actual invariant mass of the fit objects with a given flag.

Parameters

flag

The flag

Definition at line 123 of file SoftGaussMassConstraint.cc.

num1stDerivative()

double num1stDerivative ( int  ifo, int  ilocal, double  eps  )

inherited

Evaluates numerically the 1st derivative w.r.t. a parameter.

Parameters

ifo	Number of FitObject
ilocal	Local parameter number
eps	variation of local parameter

Definition at line 312 of file SoftGaussParticleConstraint.cc.

num2ndDerivative()

double num2ndDerivative ( int  ifo1, int  ilocal1, double  eps1, int  ifo2, int  ilocal2, double  eps2  )

inherited

Evaluates numerically the 2nd derivative w.r.t. 2 parameters.

Parameters

ifo1	Number of 1st FitObject
ilocal1	1st local parameter number
eps1	variation of 1st local parameter
ifo2	Number of 1st FitObject
ilocal2	1st local parameter number
eps2	variation of 2nd local parameter

Definition at line 326 of file SoftGaussParticleConstraint.cc.

print()

std::ostream & print ( std::ostream &  os ) const

virtualinherited

print object to ostream

Parameters

os	The output stream

Definition at line 76 of file BaseConstraint.cc.

secondDerivatives()

bool secondDerivatives ( int  i, int  j, double *  derivatives  ) const

overrideprotectedvirtual

Second derivatives with respect to the 4-vectors of Fit objects i and j; result false if all derivatives are zero.

Parameters

i	number of 1st FitObject
j	number of 2nd FitObject
derivatives	The result 4x4 matrix

Implements SoftGaussParticleConstraint.

Definition at line 145 of file SoftGaussMassConstraint.cc.

setFOList()

virtual void setFOList ( std::vector< ParticleFitObject * > *  fitobjects_ )

inlinevirtualinherited

Adds several ParticleFitObject objects to the list.

Parameters

fitobjects_

A list of BaseFitObject objects

Definition at line 83 of file SoftGaussParticleConstraint.h.

      {
        for (int i = 0; i < (int) fitobjects_->size(); i++) {
          fitobjects.push_back((*fitobjects_)[i]);
          flags.push_back(1);
        }
      };

setMass()

void setMass ( double  mass_ )

virtual

Sets the target mass of the constraint.

Parameters

mass_

The new mass

Definition at line 140 of file SoftGaussMassConstraint.cc.

setSigma()

double setSigma ( double  sigma_ )

virtualinherited

Sets the sigma.

Parameters

sigma_

The new sigma value

Definition at line 42 of file SoftGaussParticleConstraint.cc.

Friends And Related Function Documentation

operator<<()

std::ostream & operator<< ( std::ostream &  os, const BaseConstraint &  bc  )

related

Prints out a BaseConstraint, using its print method.

Parameters

os	The output stream
bc	The object to print

Definition at line 114 of file BaseConstraint.h.

---

The documentation for this class was generated from the following files:

• analysis/OrcaKinFit/include/SoftGaussMassConstraint.h
• analysis/OrcaKinFit/src/SoftGaussMassConstraint.cc