UncertainHelix Class Reference

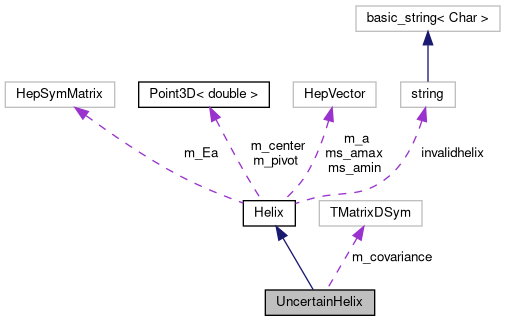
This class represents an ideal helix in perigee parameterization including the covariance matrix of the 5 perigee parameters. More...

#include <UncertainHelix.h>

Inheritance diagram for UncertainHelix:

Collaboration diagram for UncertainHelix:

Public Member Functions
	UncertainHelix ()
	Default constuctor initialising all members to zero.
	UncertainHelix (const ROOT::Math::XYZVector &position, const ROOT::Math::XYZVector &momentum, const short int charge, const double bZ, const TMatrixDSym &cartesianCovariance, const double pValue)
	Constructor initializing class with fit result. More...
	UncertainHelix (const double &d0, const double &phi0, const double &omega, const double &z0, const double &tanLambda, const TMatrixDSym &covariance, const double pValue)
	Constructor initializing class with perigee parameters. More...
TMatrixDSym	getCartesianCovariance (const double bZ_tesla=1.5) const
	Getter for the position and momentum covariance matrix. More...
double	getPValue () const
	Getter for Chi2 Probability of the track fit.
const TMatrixDSym &	getCovariance () const
	Getter for covariance matrix of perigee parameters in matrix form.
void	reverse ()
	Reverses the direction of travel of the helix in place. More...
double	passiveMoveBy (const ROOT::Math::XYZVector &by)
	Moves origin of the coordinate system (passive transformation) by the given vector. More...
double	passiveMoveBy (const double &byX, const double &byY, const double &byZ)
	Moves origin of the coordinate system (passive transformation) by the given vector. More...
const HepPoint3D &	center (void) const
	returns position of helix center(z = 0.);
const HepPoint3D &	pivot (void) const
	returns pivot position.
const HepPoint3D &	pivot (const HepPoint3D &newPivot)
	Sets pivot position.
double	radius (void) const
	returns radious of helix.
HepPoint3D	x (double dPhi=0.) const
	returns position after rotating angle dPhi in phi direction. More...
double *	x (double dPhi, double p[3]) const
	returns position after rotating angle dPhi in phi direction. More...
HepPoint3D	x (double dPhi, HepSymMatrix &Ex) const
	returns position and convariance matrix(Ex) after rotation.
Hep3Vector	direction (double dPhi=0.) const
	returns direction vector after rotating angle dPhi in phi direction.
Hep3Vector	momentum (double dPhi=0.) const
	returns momentum vector after rotating angle dPhi in phi direction.
Hep3Vector	momentum (double dPhi, HepSymMatrix &Em) const
	returns momentum vector after rotating angle dPhi in phi direction.
HepLorentzVector	momentum (double dPhi, double mass) const
	returns 4momentum vector after rotating angle dPhi in phi direction.
HepLorentzVector	momentum (double dPhi, double mass, HepSymMatrix &Em) const
	returns 4momentum vector after rotating angle dPhi in phi direction.
HepLorentzVector	momentum (double dPhi, double mass, HepPoint3D &x, HepSymMatrix &Emx) const
	returns 4momentum vector after rotating angle dPhi in phi direction.
double	dr (void) const
	Return helix parameter dr.
double	phi0 (void) const
	Return helix parameter phi0.
double	kappa (void) const
	Return helix parameter kappa.
double	dz (void) const
	Return helix parameter dz.
double	tanl (void) const
	Return helix parameter tangent lambda.
double	curv (void) const
	Return curvature of helix.
double	sinPhi0 (void) const
	Return sin phi0.
double	cosPhi0 (void) const
	Return cos phi0.
const HepVector &	a (void) const
	Returns helix parameters.
const HepVector &	a (const HepVector &newA)
	Sets helix parameters.
const HepSymMatrix &	Ea (void) const
	Returns error matrix.
const HepSymMatrix &	Ea (const HepSymMatrix &newdA)
	Sets helix paramters and error matrix.
void	set (const HepPoint3D &pivot, const HepVector &a, const HepSymMatrix &Ea)
	Sets helix pivot position, parameters, and error matrix.
void	ignoreErrorMatrix (void)
	Unsets error matrix. More...
double	bFieldZ (double bz)
	Sets/returns z componet of the magnetic field. More...
double	bFieldZ (void) const
	Returns z componet of the magnetic field.
HepMatrix	delApDelA (const HepVector &ap) const
	DAp/DA.
HepMatrix	delXDelA (double phi) const
	DX/DA.
HepMatrix	delMDelA (double phi) const
	DM/DA.
HepMatrix	del4MDelA (double phi, double mass) const
	DM4/DA.
HepMatrix	del4MXDelA (double phi, double mass) const
	DMX4/DA.

Static Public Member Functions
static void	set_limits (const HepVector &a_min, const HepVector &a_max)
	set limit for parameter "a"
static bool	set_exception (bool)
	set exception
static bool	set_print (bool)
	Set print option for debugging.

Static Public Attributes
static const double	ConstantAlpha = 222.376063
	Constant alpha for uniform field.

Private Member Functions
	ClassDef (UncertainHelix, 2)
	represents an ideal helix in perigee parameterization including covariance matrix
void	updateCache (void)
	updateCache
void	checkValid (void)
	Check whether helix parameters is valid or not. More...
void	debugPrint (void) const
	Print the helix parameters to stdout.
void	debugHelix (void) const
	Debug Helix.

Private Attributes
TMatrixDSym	m_covariance
	5x5 covariance of the perigee parameters.
Double32_t	m_pValue
	Chi2 Probability of the fit.
bool	m_matrixValid
	True: matrix valid, False: matrix not valid.
bool	m_helixValid
	True: helix valid, False: helix not valid.
double	m_bField
	Magnetic field, assuming uniform Bz in the unit of kG.
double	m_alpha
	10000.0/(speed of light)/B.
HepPoint3D	m_pivot
	Pivot.
HepVector	m_a
	Helix parameter.
HepSymMatrix	m_Ea
	Error of the helix parameter.
HepPoint3D	m_center
	Cache of the center position of Helix.
double	m_cp
	Cache of the cos phi0.
double	m_sp
	Cache of the sin phi0.
double	m_pt
	Cache of the pt.
double	m_r
	Cache of the r.
double	m_ac [5]
	Cache of the helix parameter.

Static Private Attributes
static HepVector	ms_amin
	minimum limit of Helix parameter a
static HepVector	ms_amax
	maxiimum limit of Helix parameter a
static bool	ms_check_range
	Check the helix parameter's range.
static bool	ms_print_debug
	Debug option flag.
static bool	ms_throw_exception
	Throw exception flag.
static const std::string	invalidhelix
	String "Invalid Helix".

Detailed Description

This class represents an ideal helix in perigee parameterization including the covariance matrix of the 5 perigee parameters.

The used perigee parameters are:

1. - the signed distance from the origin to the perigee. The sign is positive (negative), if the angle from the xy perigee position vector to the transverse momentum vector is +pi/2 (-pi/2). has the same sign as getPerigee().Cross(getMomentum()).Z().
2. - the angle in the xy projection between the transverse momentum and the x axis, which is in [-pi, pi]
3. - the signed curvature of the track where the sign is given by the charge of the particle
4. - z coordinate of the perigee
5. - the slope of the track in the sz plane (dz/ds)

in that exact order.

It may also store a p-value obtained from the fit of the helix.

Definition at line 36 of file UncertainHelix.h.

Constructor & Destructor Documentation

UncertainHelix() [1/2]

UncertainHelix	(	const ROOT::Math::XYZVector &	position,
		const ROOT::Math::XYZVector &	momentum,
		const short int	charge,
		const double	bZ,
		const TMatrixDSym &	cartesianCovariance,
		const double	pValue
	)

Constructor initializing class with fit result.

The given position, momentum and their covariance matrix are extrapolated to the perigee assuming a homogeneous magnetic field in the z direction.

Parameters

position	Position of the track at the perigee.
momentum	Momentum of the track at the perigee.
charge	Charge of the particle.
bZ	Magnetic field to be used for the calculation of the curvature;
cartesianCovariance	6x6 Covariance matrix for position and momentum of the track at the perigee.
pValue	p-value of the fit. It is assumed, that the B-field is parallel to the z-Axis.

Definition at line 24 of file UncertainHelix.cc.

                                                    :
  Helix(ROOT::Math::XYZVector(0.0, 0.0, position.Z()), momentum, charge, bZ),
  m_covariance(cartesianCovariance), // Initialize the covariance matrix to the 6x6 covariance and reduce it afterwards
  m_pValue(pValue)
{
  // Maybe push these out of this function:
  // Indices of the cartesian coordinates
  const int iX = 0;
  const int iY = 1;
  const int iZ = 2;
  const int iPx = 3;
  const int iPy = 4;
  const int iPz = 5;
 
  // We initialised the m_covariance to the cartesian covariance and
  // reduce it now to the real 5x5 matrix that should be there.
 
  // 1. Rotate to a system where phi0 = 0
  TMatrixD jacobianRot(6, 6);
  jacobianRot.Zero();
 
  const double px = momentum.X();
  const double py = momentum.Y();
  const double pt = hypot(px, py);
  const double cosPhi0 = px / pt;
  const double sinPhi0 = py / pt;
 
  // Passive rotation matrix by phi0:
  jacobianRot(iX, iX) = cosPhi0;
  jacobianRot(iX, iY) = sinPhi0;
  jacobianRot(iY, iX) = -sinPhi0;
  jacobianRot(iY, iY) = cosPhi0;
  jacobianRot(iZ, iZ) = 1.0;
 
  jacobianRot(iPx, iPx) = cosPhi0;
  jacobianRot(iPx, iPy) = sinPhi0;
  jacobianRot(iPy, iPx) = -sinPhi0;
  jacobianRot(iPy, iPy) = cosPhi0;
  jacobianRot(iPz, iPz) = 1.0;
 
  m_covariance.Similarity(jacobianRot);
 
  // 2. Translate to perigee parameters on the position
  const double pz = momentum.Z();
  const double invPt = 1 / pt;
  const double invPtSquared = invPt * invPt;
  const double alpha = getAlpha(bZ);
 
  TMatrixD jacobianToHelixParameters(5, 6);
  jacobianToHelixParameters.Zero();
 
  jacobianToHelixParameters(iD0, iY) = -1;
  jacobianToHelixParameters(iPhi0, iX) = charge * invPt / alpha;
  jacobianToHelixParameters(iPhi0, iPy) = invPt;
  jacobianToHelixParameters(iOmega, iPx) = -charge * invPtSquared / alpha;
  jacobianToHelixParameters(iTanLambda, iPx) = - pz * invPtSquared;
  jacobianToHelixParameters(iTanLambda, iPz) = invPt;
  jacobianToHelixParameters(iZ0, iX) = - pz * invPt;
  jacobianToHelixParameters(iZ0, iZ) = 1;
  m_covariance.Similarity(jacobianToHelixParameters);
 
  // The covariance m_covariance is now the correct 5x5 covariance matrix.
  assert(m_covariance.GetNrows() == 5);
 
  // 3. Extrapolate to the origin.
  /* const double arcLength2D = */ passiveMoveBy(-position.X(), -position.Y(), 0.0);
}

UncertainHelix() [2/2]

UncertainHelix	(	const double &	d0,
		const double &	phi0,
		const double &	omega,
		const double &	z0,
		const double &	tanLambda,
		const TMatrixDSym &	covariance,
		const double	pValue
	)

Constructor initializing class with perigee parameters.

Parameters

d0	The signed distance from the origin to the perigee. The sign is positive (negative), if the angle from the xy perigee position vector to the transverse momentum vector is +pi/2 (-pi/2). d0 has the same sign as getPosition().Cross(getMomentum()).Z().
phi0	The angle between the transverse momentum and the x axis and in [-pi, pi]
omega	The signed curvature of the track where the sign is given by the charge of the particle
z0	The z coordinate of the perigee.
tanLambda	The slope of the track in the sz plane (dz/ds)
covariance	5x5 Covariance matrix for the five helix parameters. Indices correspond to the order d0, phi0, omega, z0, tanLambda.
pValue	p-value of the Helix fit

Definition at line 98 of file UncertainHelix.cc.

Member Function Documentation

bFieldZ()

double bFieldZ ( double  bz )

inlineinherited

Sets/returns z componet of the magnetic field.

Parameters

[in]

bz

z-component of the magnetic field.

Attention

Helix param. alpha is also stored.

Definition at line 473 of file Helix.h.

    {
      DEBUG_HELIX;
      m_bField = a;
      m_alpha = 10000. / 2.99792458 / m_bField;
      updateCache();
      return m_bField;
    }

checkValid()

void checkValid ( void  )

privateinherited

Check whether helix parameters is valid or not.

Sets m_helixValid.

Definition at line 895 of file Helix.cc.

{
 
  if (!ms_check_range) return;
  const double adr   = fabs(m_a[0]);
  const double acpa   = fabs(m_a[2]);
  if (!(adr >= ms_amin[0] && adr <= ms_amax[0])) {
    m_helixValid = false;
  } else if (!(acpa >= ms_amin[2] && acpa <= ms_amax[2])) {
    m_helixValid = false;
  } else {
    m_helixValid = true;
  }
  if (!m_helixValid) {
    if (m_a[0] != 0.0 || m_a[1] != 0.0 || m_a[2] != 0.0 ||
        m_a[3] != 0.0 || m_a[4] != 0.0) {
      DEBUG_PRINT;
    }
  }
 
}

getCartesianCovariance()

TMatrixDSym getCartesianCovariance

(

const double

bZ_tesla = 1.5

)

const

Getter for the position and momentum covariance matrix.

Note

Because the position and momentum covariance matrix is regenerated from a 5x5 perigee parameter covariance matrix there is necessarily a missing rank in the resulting matrix. The rank has to be filled by a convention essentially expressing, which points around the perigee are considered to be at s = 0. For backwards compatability with the original Belle experiment we apply the convention used there. See the Belle II note for more details.

Parameters

bZ_tesla

Magnetic field to be used for the calculation from the curvature;

1. Rotate to the right phi0

Definition at line 113 of file UncertainHelix.cc.

ignoreErrorMatrix()

void ignoreErrorMatrix ( void  )

inherited

Unsets error matrix.

Error calculations will be ignored after this function call until an error matrix be set again. 0 matrix will be return as a return value for error matrix when you call functions which returns an error matrix.

Definition at line 872 of file Helix.cc.

passiveMoveBy() [1/2]

double passiveMoveBy	(	const double &	byX,
		const double &	byY,
		const double &	byZ
	)

Moves origin of the coordinate system (passive transformation) by the given vector.

Updates the helix inplace.

Parameters

byX	X displacement by which the origin of the coordinate system should be moved.
byY	Y displacement by which the origin of the coordinate system should be moved.
byZ	Z displacement by which the origin of the coordinate system should be moved.

Returns

The double value is the two dimensional arc length, which has the be traversed from the old perigee to the new.

Definition at line 198 of file UncertainHelix.cc.

passiveMoveBy() [2/2]

double passiveMoveBy ( const ROOT::Math::XYZVector &  by )

inline

Moves origin of the coordinate system (passive transformation) by the given vector.

Updates the helix inplace.

Parameters

by	Vector by which the origin of the coordinate system should be moved.

Returns

The double value is the two dimensional arc length, which has the be traversed from the old perigee to the new.

Definition at line 117 of file UncertainHelix.h.

    { return passiveMoveBy(by.X(), by.Y(), by.Z()); }

reverse()

void reverse

(

)

Reverses the direction of travel of the helix in place.

The same points that are located on the helix stay are the same after the transformation, but have the opposite two dimensional arc length associated to them. The momentum at each point is reversed. The charge sign is changed to its opposite by this transformation.

Definition at line 182 of file UncertainHelix.cc.

x() [1/2]

double * x ( double  dPhi, double  p[3]  ) const

inherited

returns position after rotating angle dPhi in phi direction.

x = x0 + dr * cos(phi0) + (alpha / kappa) * (cos(phi0) - cos(phi0+phi)) y = y0 + dr * sin(phi0) + (alpha / kappa) * (sin(phi0) - sin(phi0+phi)) z = z0 + dz - (alpha / kappa) * tan(lambda) * phi

Returns

double[3]

Definition at line 216 of file Helix.cc.

x() [2/2]

HepPoint3D x ( double  dPhi = 0. ) const

inherited

returns position after rotating angle dPhi in phi direction.

x = x0 + dr * cos(phi0) + (alpha / kappa) * (cos(phi0) - cos(phi0+phi)) y = y0 + dr * sin(phi0) + (alpha / kappa) * (sin(phi0) - sin(phi0+phi)) z = z0 + dz - (alpha / kappa) * tan(lambda) * phi

Returns

HepPoint3D

Definition at line 197 of file Helix.cc.

---

The documentation for this class was generated from the following files:

• framework/dataobjects/include/UncertainHelix.h
• framework/dataobjects/src/UncertainHelix.cc